When ultraviolet radiation of a certain frequency falls on a potassium target, the photoelectrons released can be stopped completely by a retarding potential of 0.6 V. If the frequency of the radiation is increased by 10%, this stopping potential rises to 0.9 V. The work function of potassium is
2.0 eV
2.4 eV
3.0 eV
2.8 eV
The correct Answer is:B
To solve the problem, we will use the concepts of photoelectric effect and the equations relating to the kinetic energy of photoelectrons and the work function of the material.
1. Understanding the Problem:
We have a potassium target exposed to ultraviolet (UV) radiation of a certain frequency. The stopping potential required to stop the emitted photoelectrons is given as 0.6 V. When the frequency of the radiation is increased by 10%, the stopping potential increases to 0.9 V. We need to find the work function (φ) of potassium.
2. Using the Photoelectric Equation:
The energy of the incident photons can be expressed using the equation:
E=hf
where h is Planck's constant and f is the frequency of the radiation.
3. Relating Kinetic Energy and Stopping Potential:
The maximum kinetic energy (K.E.) of the emitted photoelectrons can be expressed as:
K.E.=eVs
where e is the charge of the electron and Vs is the stopping potential.
For the first case (stopping potential = 0.6 V):
K.E.=e⋅0.6 V
Thus, we can write:
hf=e⋅0.6+φ(1)
4. Increasing the Frequency by 10%:
When the frequency is increased by 10%, the new frequency f′ is:
f′=1.1f
The energy of the photons at this new frequency is:
E′=hf′=h(1.1f)=1.1hf
The new stopping potential is 0.9 V, so:
K.E.=e⋅0.9 V
This gives us the second equation:
1.1hf=e⋅0.9+φ(2)
5. Setting Up the Equations:
We now have two equations:
- From equation (1): hf=e⋅0.6+φ
- From equation (2): 1.1hf=e⋅0.9+φ
6. Substituting Equation (1) into Equation (2):
We can express hf from equation (1):
hf=e⋅0.6+φ
Substitute this into equation (2):
1.1(e⋅0.6+φ)=e⋅0.9+φ
7. Expanding and Rearranging:
Expanding the left side:
1.1e⋅0.6+1.1φ=e⋅0.9+φ
Rearranging gives:
1.1e⋅0.6−e⋅0.9=φ−1.1φ
Simplifying:
0.66e−0.9e=−0.1φ
−0.24e=−0.1φ
Thus:
φ=0.24e0.1=2.4 eV
8. Conclusion:
The work function of potassium is:
φ=2.4 eV
We have a potassium target exposed to ultraviolet (UV) radiation of a certain frequency. The stopping potential required to stop the emitted photoelectrons is given as 0.6 V. When the frequency of the radiation is increased by 10%, the stopping potential increases to 0.9 V. We need to find the work function (φ) of potassium.
The energy of the incident photons can be expressed using the equation:
E=hf
where h is Planck's constant and f is the frequency of the radiation.
The maximum kinetic energy (K.E.) of the emitted photoelectrons can be expressed as:
K.E.=eVs
where e is the charge of the electron and Vs is the stopping potential.
K.E.=e⋅0.6 V
Thus, we can write:
hf=e⋅0.6+φ(1)
When the frequency is increased by 10%, the new frequency f′ is:
f′=1.1f
The energy of the photons at this new frequency is:
E′=hf′=h(1.1f)=1.1hf
K.E.=e⋅0.9 V
This gives us the second equation:
1.1hf=e⋅0.9+φ(2)
We now have two equations:
- From equation (1): hf=e⋅0.6+φ
- From equation (2): 1.1hf=e⋅0.9+φ
We can express hf from equation (1):
hf=e⋅0.6+φ
Substitute this into equation (2):
1.1(e⋅0.6+φ)=e⋅0.9+φ
Expanding the left side:
1.1e⋅0.6+1.1φ=e⋅0.9+φ
Rearranging gives:
1.1e⋅0.6−e⋅0.9=φ−1.1φ
Simplifying:
0.66e−0.9e=−0.1φ
−0.24e=−0.1φ
Thus:
φ=0.24e0.1=2.4 eV
The work function of potassium is:
φ=2.4 eV
Topper's Solved these Questions
Similar Questions
When a radiation of energy 5eV falls on a surface,the emitted photoelectrons have a maximum kinetic energy of 3eV .The stopping potential is
View SolutionWhen photons of energy 5 eV fall on the surface of a metal, the emitted photoelectrons are stopped by a cut off potential of 1.6V. The work function of given metal is______.
View Solution
Knowledge Check
On a photosensitive material, when frequency of incident radiation is increased by 30% kinetic energy of emitted photoelectrons increases from 0.4eV to 0.9eV. The work function of the surface is
A1 eVB1.267eVC1.4eVD1.8eVWhich of the following is the graph between the frequency (v) of the incident radiations and the stopping potential ?
A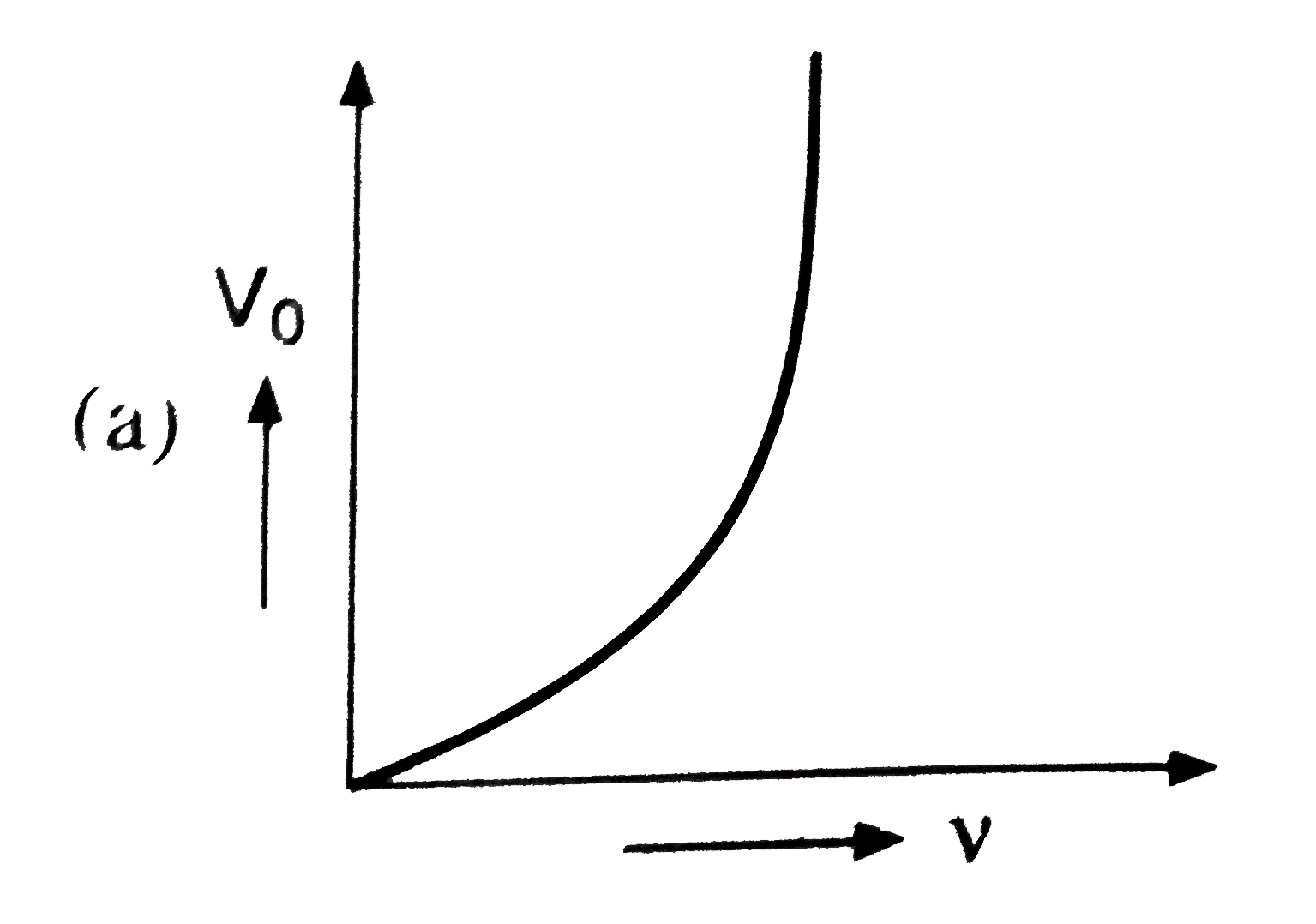
B
C
D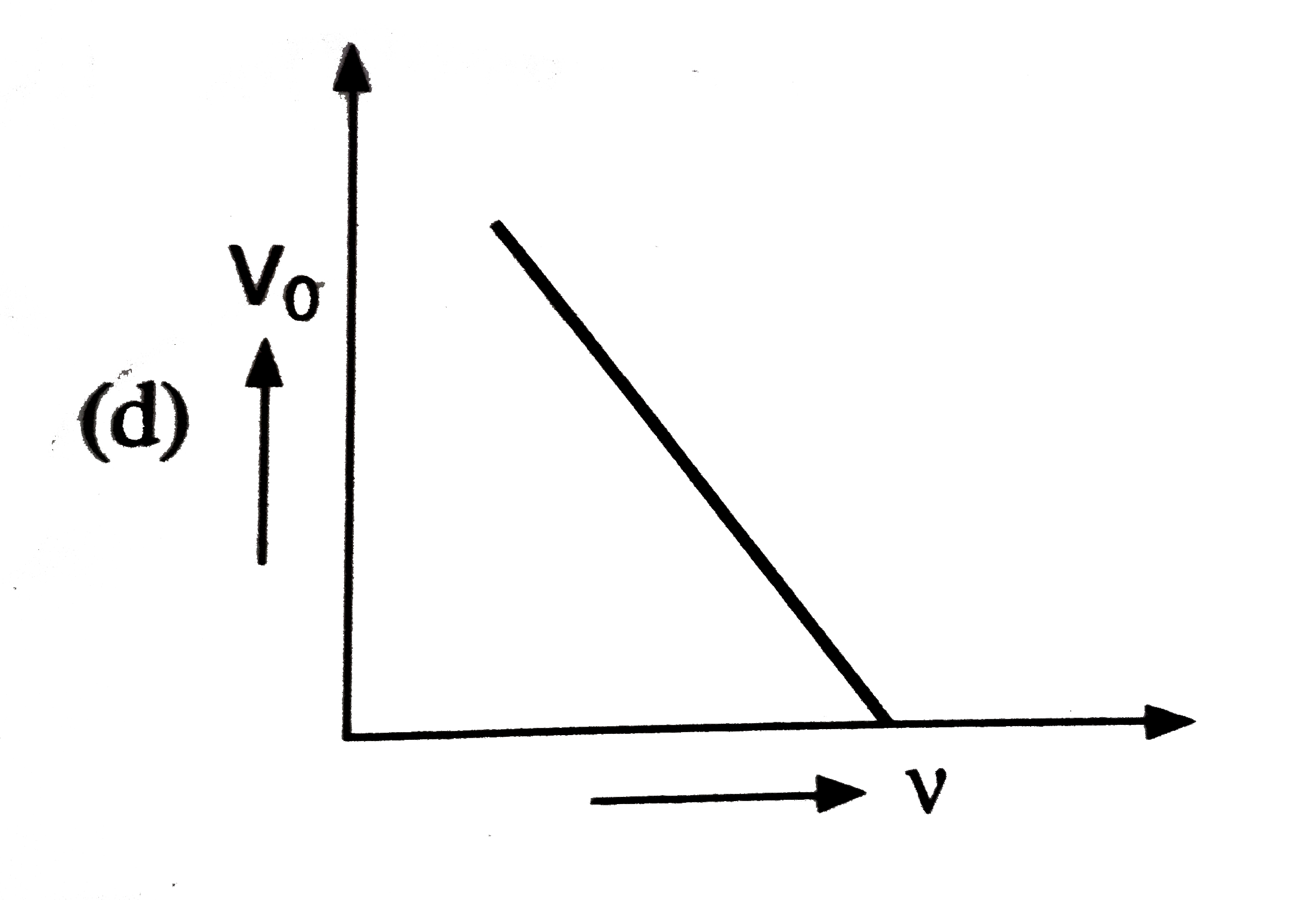
The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces A and B . The graphs show that work function of A is
AGreater than that of BBSmaller than that of BCEqual to that of BDNo inference can be drawn about their work functions from the given graphs
if the speed of photoelectrons is 104 m/s, what should be the frequency of the incident radiation on a potassium metal ? Given : Work function of potassium =2.3 eV
View SolutionWhen light of frequency v1 incident on a metal with work function W0 (where hv1>W0), the photocurrent falls to zero at a stopping potential of V1. If the frequency of light is increased to v2, the stopping potential changes to V2. Therefore, the charge of an electron is given by
View SolutionIn aphotocell frequency of incident radiation is increased by keeping other factors constant (v>v0), the stopping potential
View SolutionFor intensity I of a light of wavelength 5000Å the photoelectron saturation current is 0.40μA and stopping potential is 1.36V , the work function of metal is
View SolutionIn an experiment on photoelectric effect the frequency f of the incident light is plotted against the stopping potential V0. The work function of the metal is given by ( e is the electronic charge)
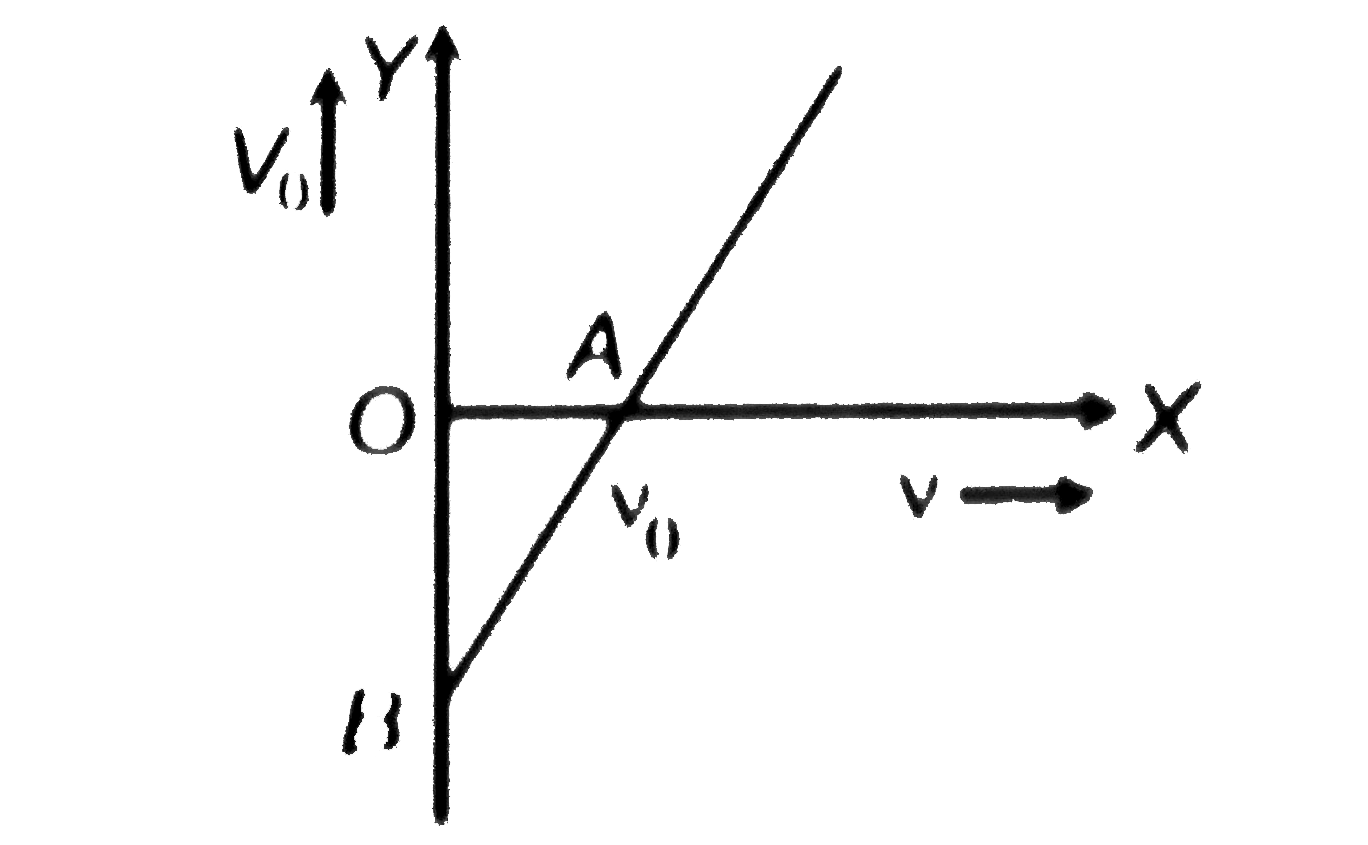
View Solution