If ∠A and ∠P are acute angle such that tanA=tanP, then show that ∠A=∠P.
Video Solution
Text Solution
Let we create a right angle triangle ABP with the given details.
Please refer to video to see the triangle.
Then,
tanA=BPAB
tanP=ABBP
It is given,
tanA=tanP
∴BPAB=ABBP
⇒BP2=AB2
⇒BP=AB
We know, opposite angles of equal sides are also equal.
∴∠A=∠P
|
Similar Questions
Knowledge Check
If tanA=cotB and angles A and B are acute, then
AA=BBA=90∘+BCB=90∘+ADA+B=90∘
If A and B are acute angles such that tanA=cotB , then show that A+B=90∘.
View SolutionIf ∠A and ∠B are supplementary angles. If 4∠A=5∠B, then find ∠A and ∠B.
View SolutionGiven that ∠A and ∠B are supplementary angles. If ∠A:∠B=7:8, then find ∠A and ∠B.
View SolutionGiven that ∠A and ∠B are complementary angles. If ∠A=∠B+20∘, then find ∠A and ∠B
View SolutionGiving reason show that
∠x=∠a+∠b
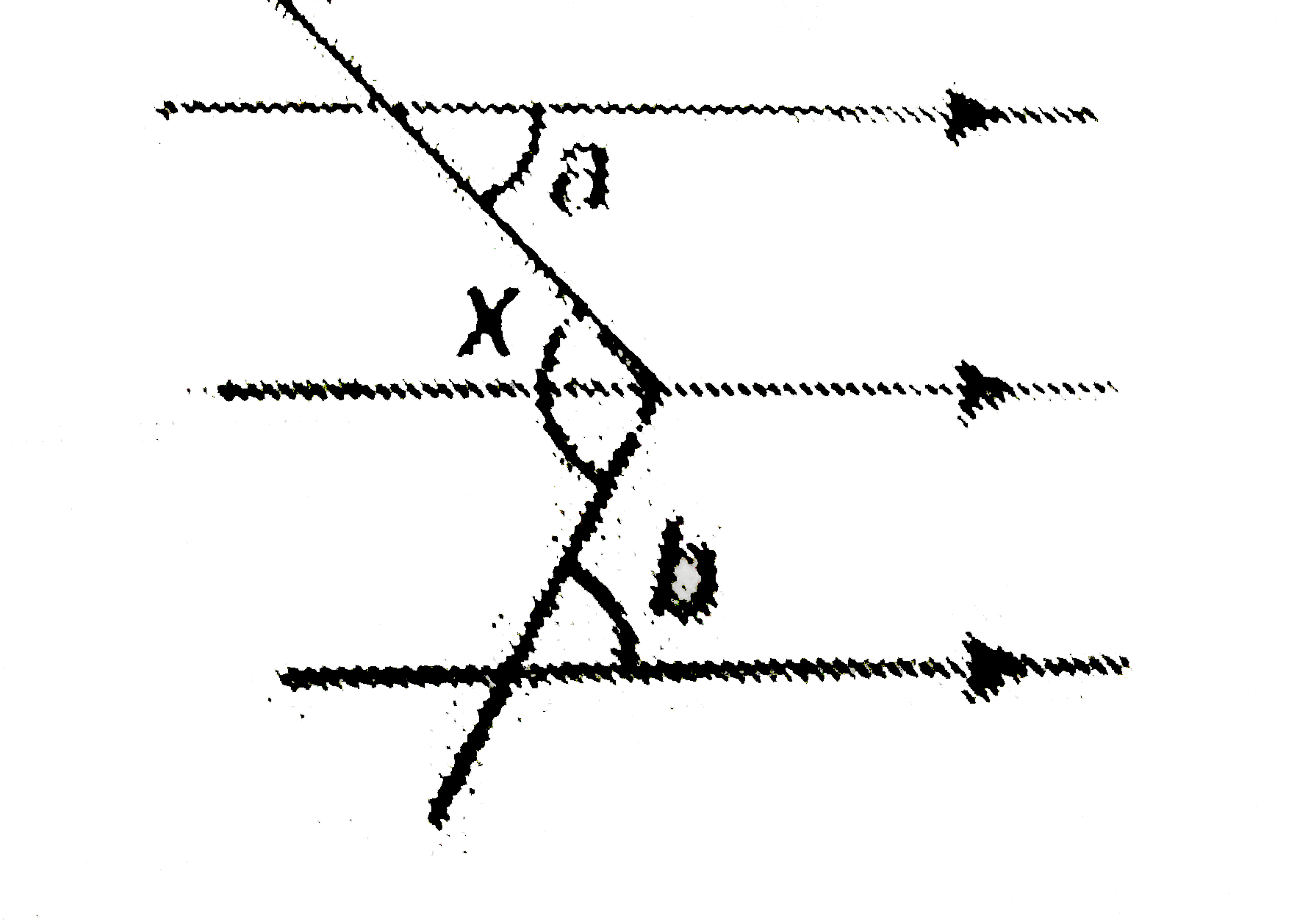
View SolutionGiving reason show that
∠x=∠a+∠b

View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
View Solution
