If ∠A and ∠P are acute angle such that tanA=tanP, then show that ∠A=∠P.
Step by step video & image solution for If angleA and angleP are acute angle such that tanA=tanP, then show that angleA=angleP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If tanA=cotB and angles A and B are acute, then
AA=BBA=90∘+BCB=90∘+ADA+B=90∘
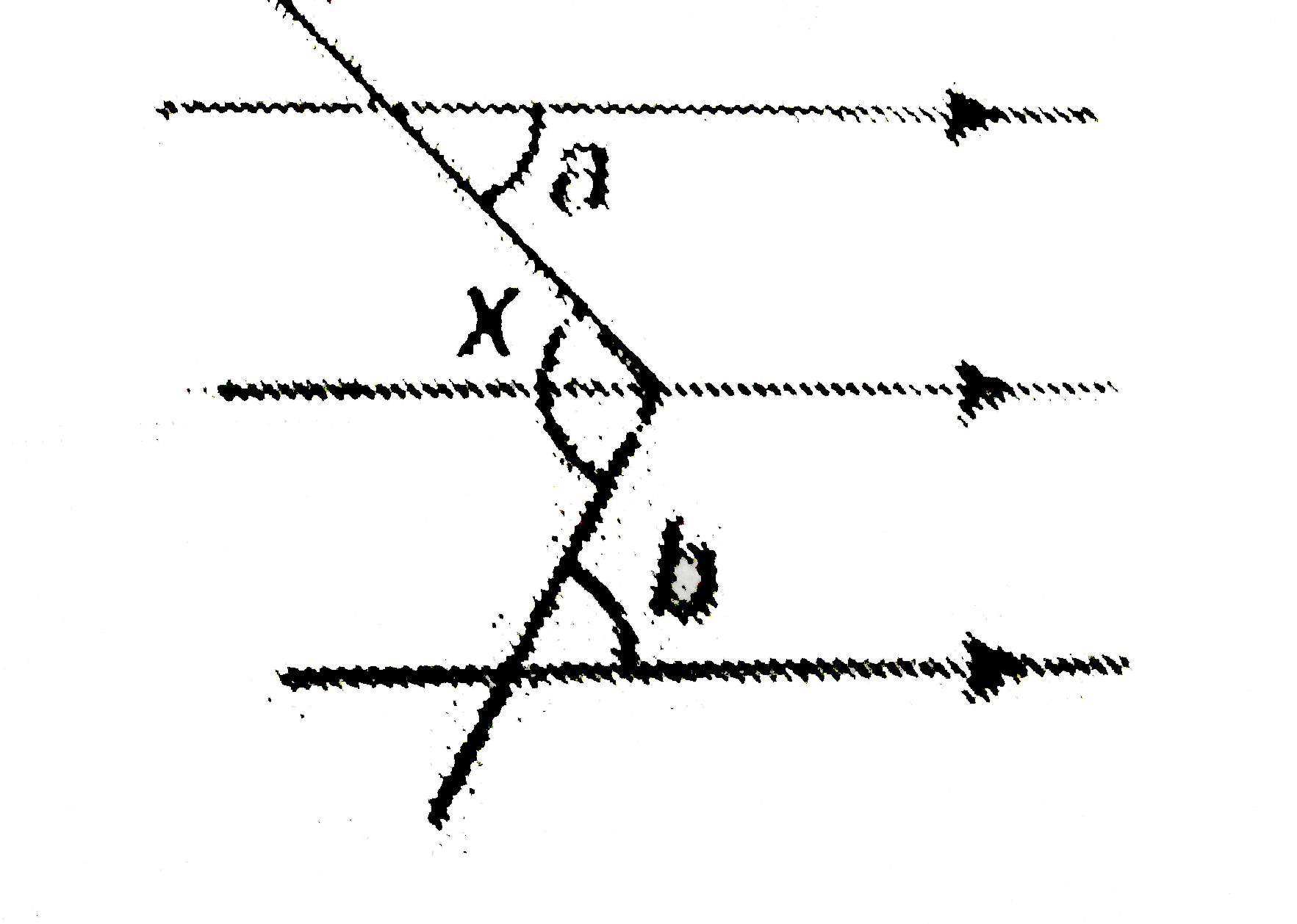
Giving reason show that
∠x=∠a+∠b
View SolutionIf A and B are acute angles such that tanA=12 , tanB=13 and tan(A+B)=tanA+tan B1−tanAtanB , find A+B .
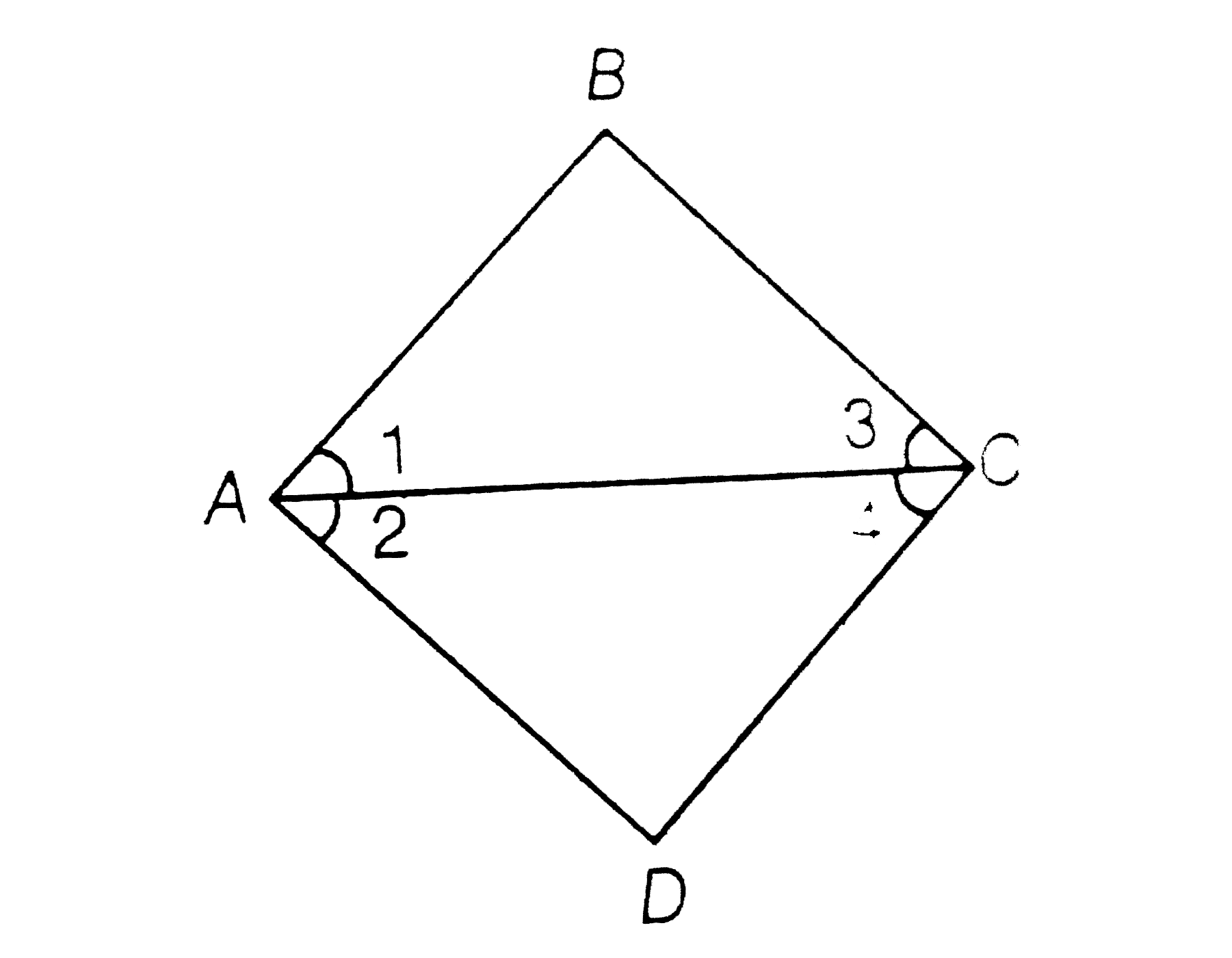
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
View SolutionIn an acute-angled triangle ABC, tanA+tanB+tanC
View SolutionIn figure, ∠B<∠A and ∠C<∠D. Show that AD<BC.
View SolutionIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D of R and of ∠Dand∠A at S, then PQRS is a (A) Rectangle (B) Rhombus (C) Parallelogram (D) Quadrilateral whose opposite angles are supplementary
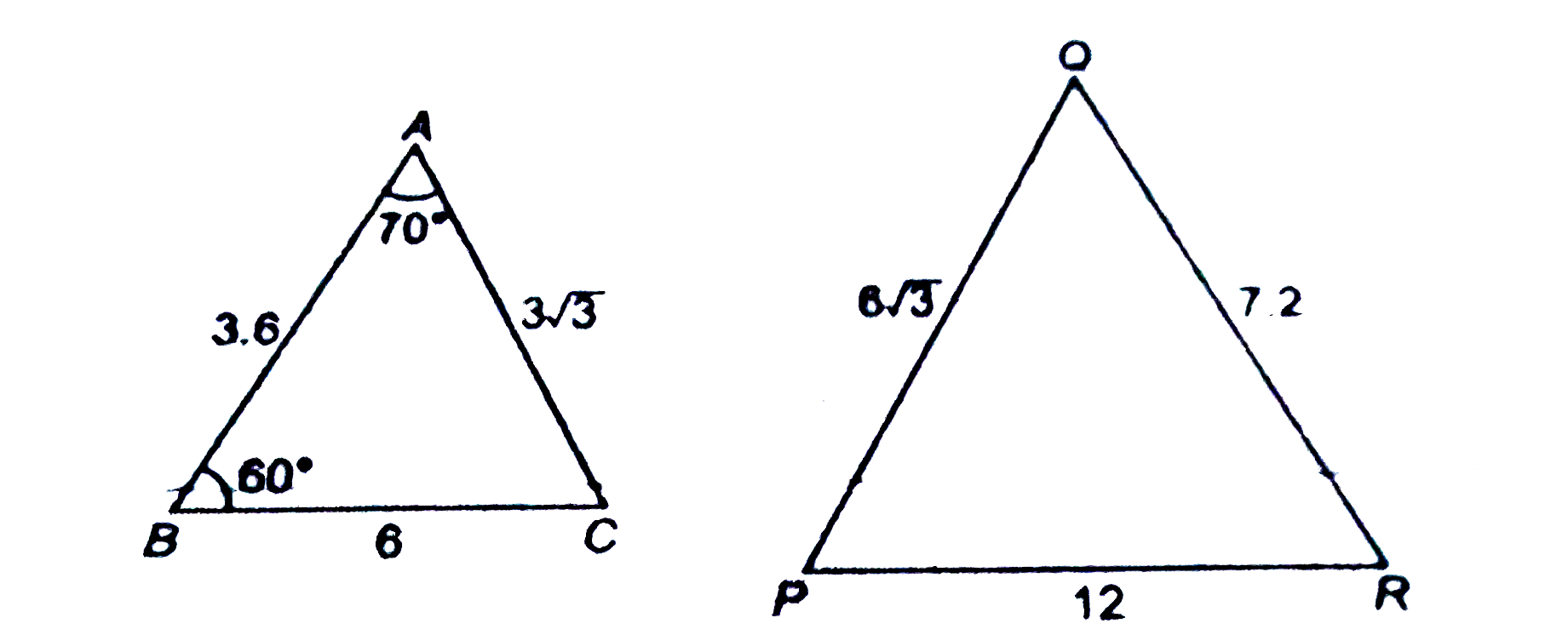
View SolutionFind ∠P in the figure below.
View Solution