Two coaxial rings, each of radius R, made of thin wire are separated by a small distance l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
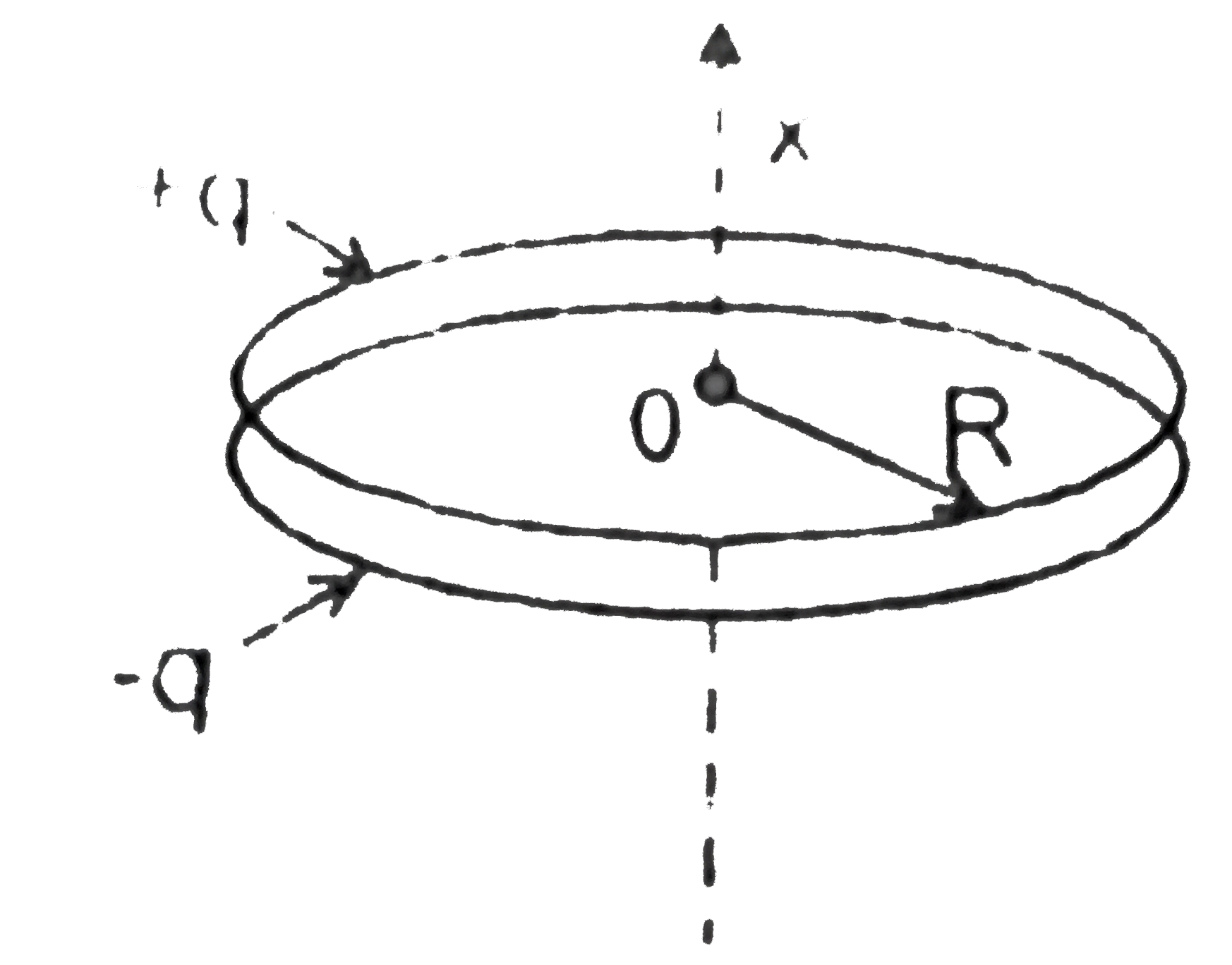
The correct Answer is:ϕ=ql4πε0x(R2+x2)3/2=Ex=ql4πε0R2−2x2(R2+x2)5/2 where Ex is the projection of the vector →E on the x-axis The fnctions are plottted in figure If |x|gtgtR, then ω≈ql4πε0x2andEx≈ql2πε0x3
(##GALPHYV03AECAC01E01232_O01##)
Step by step video, text & image solution for Two coaxial rings, each of radius R, made of thin wire are separated by a small distance l(l lt lt R) and carry the charges q and -q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x| gt gt R by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs
40 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
Two coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R

View SolutionTwo co-axisal rings, each of radius R, are separated by a small distance l(ltltR) and carry charges q and -q.Find the electric potential and field at a point on the axis at a distance x from the midpoint between the rings,
View Solution
Knowledge Check
Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
A(a) q2π∈0[1R−1√R2−d2]B(b) qR4π∈0d2C(c) q4π∈0[1R−1√R2+d2]D(d) zeroThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A14πε0q3√3R2B14πε02q3R2C14πε02q3√3R2D14πε03q2√2R2
An electric capacitor consists of this round parallel plates. each of radius R, separated by a distance l(l<<R) and uniformly charged with surface densities σ and −σ . Find the potential of the electirc field and the magnitude of tis strength vector at the axes of the capacitor as functions of a distanace x from the plates if x>>l. Investigate and obtained expressions at x>>R.
View SolutionA very thin round plate of radius R carrying a uniform surface charge density σ is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l→0 and l>>R.
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

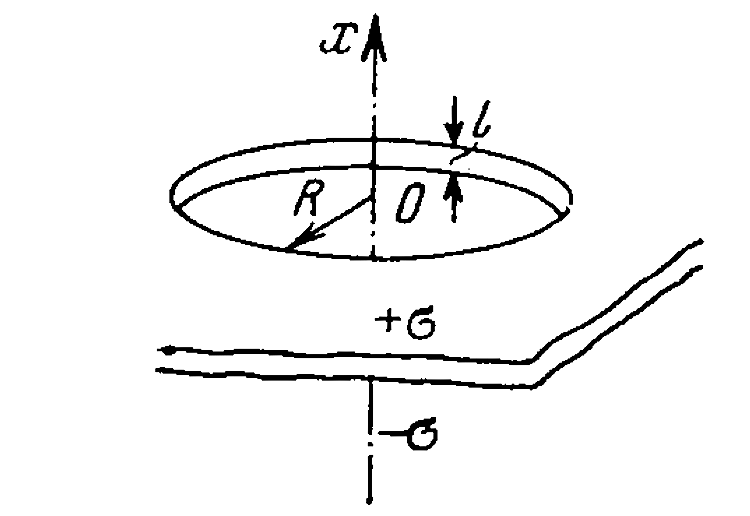
View SolutionTwo infinite planes sepated by a distance l carrying a uniform surface charge of densities σ and −σ. The planes have round coaxial holes of radius R, with l<<R. Taking the origin O and the x cordinates axis as shown in the figure, find the potentail of the electric field and the projection of its strength vector Ex on the area of the system as functions of the x cordiante. Draw the appoximate plot φ(x).
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View Solution
