A uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a/3 from the edge. The rod is released from rest. If the rod slips after it turned an angle θ, find the coefficient of friction between the rod and the table.
To solve the problem, we need to analyze the motion of the uniform rod as it slips off the edge of the table after being released from rest. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Setup
The rod has a length of 2a and is placed horizontally on the edge of a table. The center of mass of the rod is initially at a distance of a3 from the edge of the table.
Step 2: Identify Forces Acting on the Rod
When the rod is released, the forces acting on it include:
- The weight of the rod, \( Mg \), acting downwards at the center of mass.
- The normal force \( N \) acting upwards at the edge of the table.
- The frictional force \( F_f \) acting horizontally at the edge of the table.
Step 3: Determine the Angle of Rotation
As the rod rotates and slips, it turns through an angle \( \theta \). The center of mass will drop vertically as the rod rotates.
Step 4: Calculate the Distance Traveled by the Center of Mass
Using trigonometry, the vertical distance \( y \) traveled by the center of mass when the rod has turned through an angle \( \theta \) is given by:
\(
y = \frac{a}{3} \sin \theta
\)
Step 5: Calculate the Potential Energy Loss
The potential energy lost by the center of mass as it drops by distance \( y \) is:
\(
\Delta PE = Mg \cdot y = Mg \cdot \left(\frac{a}{3} \sin \theta\right)
\)
Step 6: Relate Potential Energy Loss to Kinetic Energy
The potential energy lost converts into kinetic energy of the rod. The kinetic energy \( KE \) of the rod can be expressed as:
\(
KE = \frac{1}{2} I \omega^2
\)
where \( I \) is the moment of inertia about the center of mass and \( \omega \) is the angular velocity.
Step 7: Calculate the Moment of Inertia
The moment of inertia \( I \) of the rod about its center of mass is given by:
\(
I = \frac{1}{12} M (2a)^2 = \frac{1}{3} Ma^2
\)
Using the parallel axis theorem, the moment of inertia about the edge of the table is:
\(
I_{edge} = I + Md^2 = \frac{1}{3} Ma^2 + M\left(\frac{a}{3}\right)^2 = \frac{1}{3} Ma^2 + \frac{1}{9} Ma^2 = \frac{4}{9} Ma^2
\)
Step 8: Set Up the Energy Equation
Equating potential energy loss to kinetic energy gives:
\(
Mg \cdot \left(\frac{a}{3} \sin \theta\right) = \frac{1}{2} \cdot \frac{4}{9} Ma^2 \omega^2
\)
Step 9: Solve for Angular Velocity
From the above equation, we can solve for \( \omega^2 \):
\(
\omega^2 = \frac{3g \sin \theta}{2a}
\)
Step 10: Calculate the Acceleration and Friction
The frictional force can be expressed as:
\(
F_f = \mu N
\)
where \( \mu \) is the coefficient of friction. The normal force \( N \) can be expressed as:
\(
N = Mg \cos \theta
\)
Using Newton's second law, we can relate the forces acting on the rod to the acceleration.
Step 11: Find the Coefficient of Friction
By analyzing the forces and using the equations derived, we can find:
\(
\mu = \frac{3g \sin \theta}{4g \cos \theta} = \frac{3}{4} \tan \theta
\)
Final Result
Thus, the coefficient of friction \( \mu \) between the rod and the table is:
\(
\mu = \frac{3}{4} \tan \theta
\)
The rod has a length of 2a and is placed horizontally on the edge of a table. The center of mass of the rod is initially at a distance of a3 from the edge of the table.
When the rod is released, the forces acting on it include:
- The weight of the rod, \( Mg \), acting downwards at the center of mass.
- The normal force \( N \) acting upwards at the edge of the table.
- The frictional force \( F_f \) acting horizontally at the edge of the table.
As the rod rotates and slips, it turns through an angle \( \theta \). The center of mass will drop vertically as the rod rotates.
Using trigonometry, the vertical distance \( y \) traveled by the center of mass when the rod has turned through an angle \( \theta \) is given by:
\(
y = \frac{a}{3} \sin \theta
\)
The potential energy lost by the center of mass as it drops by distance \( y \) is:
\(
\Delta PE = Mg \cdot y = Mg \cdot \left(\frac{a}{3} \sin \theta\right)
\)
The potential energy lost converts into kinetic energy of the rod. The kinetic energy \( KE \) of the rod can be expressed as:
\(
KE = \frac{1}{2} I \omega^2
\)
where \( I \) is the moment of inertia about the center of mass and \( \omega \) is the angular velocity.
The moment of inertia \( I \) of the rod about its center of mass is given by:
\(
I = \frac{1}{12} M (2a)^2 = \frac{1}{3} Ma^2
\)
Using the parallel axis theorem, the moment of inertia about the edge of the table is:
\(
I_{edge} = I + Md^2 = \frac{1}{3} Ma^2 + M\left(\frac{a}{3}\right)^2 = \frac{1}{3} Ma^2 + \frac{1}{9} Ma^2 = \frac{4}{9} Ma^2
\)
Equating potential energy loss to kinetic energy gives:
\(
Mg \cdot \left(\frac{a}{3} \sin \theta\right) = \frac{1}{2} \cdot \frac{4}{9} Ma^2 \omega^2
\)
From the above equation, we can solve for \( \omega^2 \):
\(
\omega^2 = \frac{3g \sin \theta}{2a}
\)
The frictional force can be expressed as:
\(
F_f = \mu N
\)
where \( \mu \) is the coefficient of friction. The normal force \( N \) can be expressed as:
\(
N = Mg \cos \theta
\)
Using Newton's second law, we can relate the forces acting on the rod to the acceleration.
By analyzing the forces and using the equations derived, we can find:
\(
\mu = \frac{3g \sin \theta}{4g \cos \theta} = \frac{3}{4} \tan \theta
\)
Thus, the coefficient of friction \( \mu \) between the rod and the table is:
\(
\mu = \frac{3}{4} \tan \theta
\)
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A thin rod of mass m and length 2l is placed horizontally and perpendicular to a horizontal rough nail, as shown in figure and set free. The point of contanct of the rod with the nails is l/3 distance away form the centre of rod. If the rod starts slipping when it forms an angle θ with the horizontal and the coefficient of friction of rod with nails is μ, then find μtanθ.
 View Solution
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pml - Question 2 - Select One
A uniform rod o length one meter is bent at its midpoint to make 90∘. The distance of centre of mass from the centre of rod is (in cm)
A20.2B13.4C15D17.6 - Question 3 - Select One
A uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.View SolutionA uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
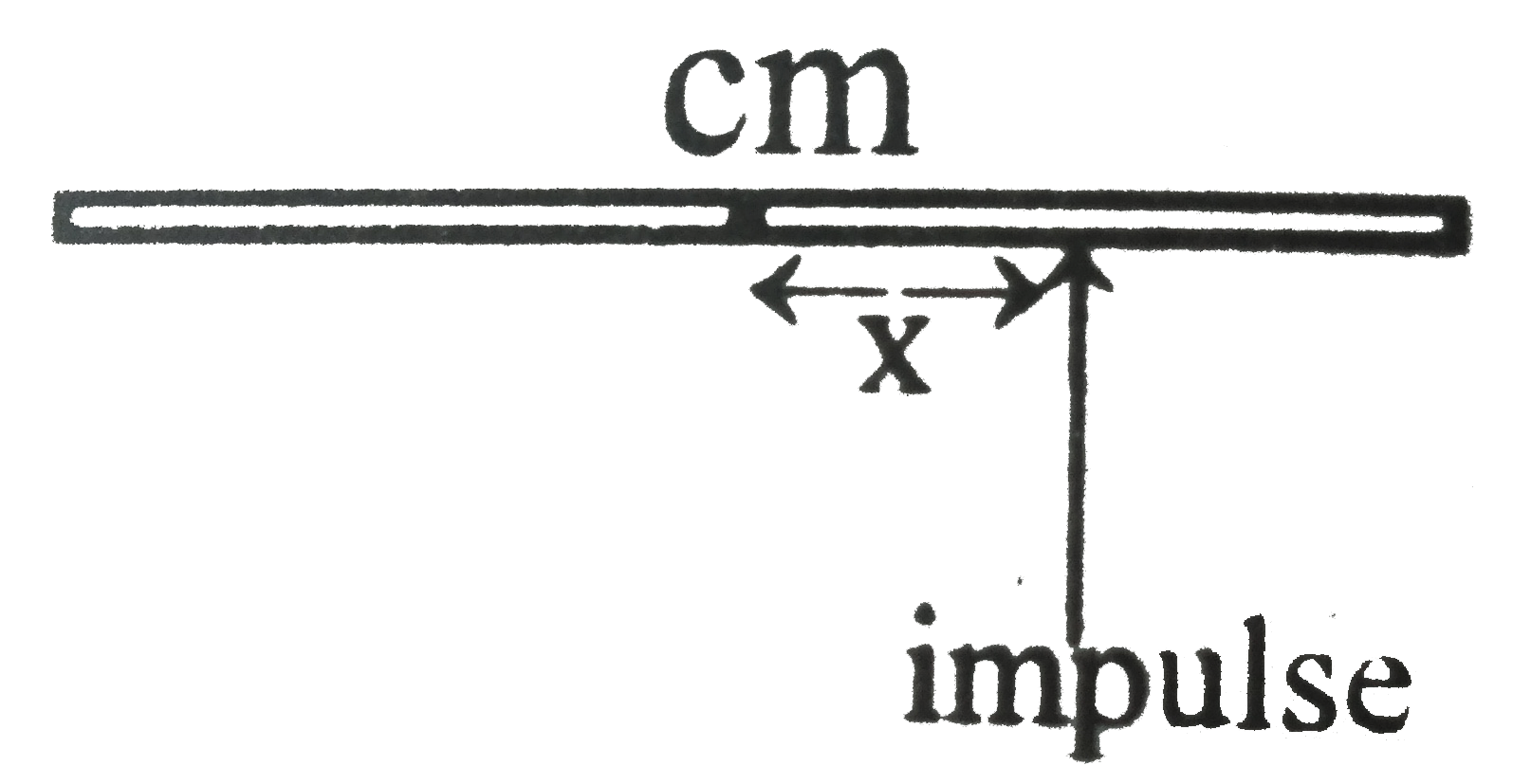 .View Solution
.View SolutionA uniform thin rod of length 2L and mass m lies on a horizontal table. A horizontal impulse J is given to the rod at one red. There is no friction. The total kinetic energy of the rod just after the impulse will be
View SolutionA uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
View Solution

