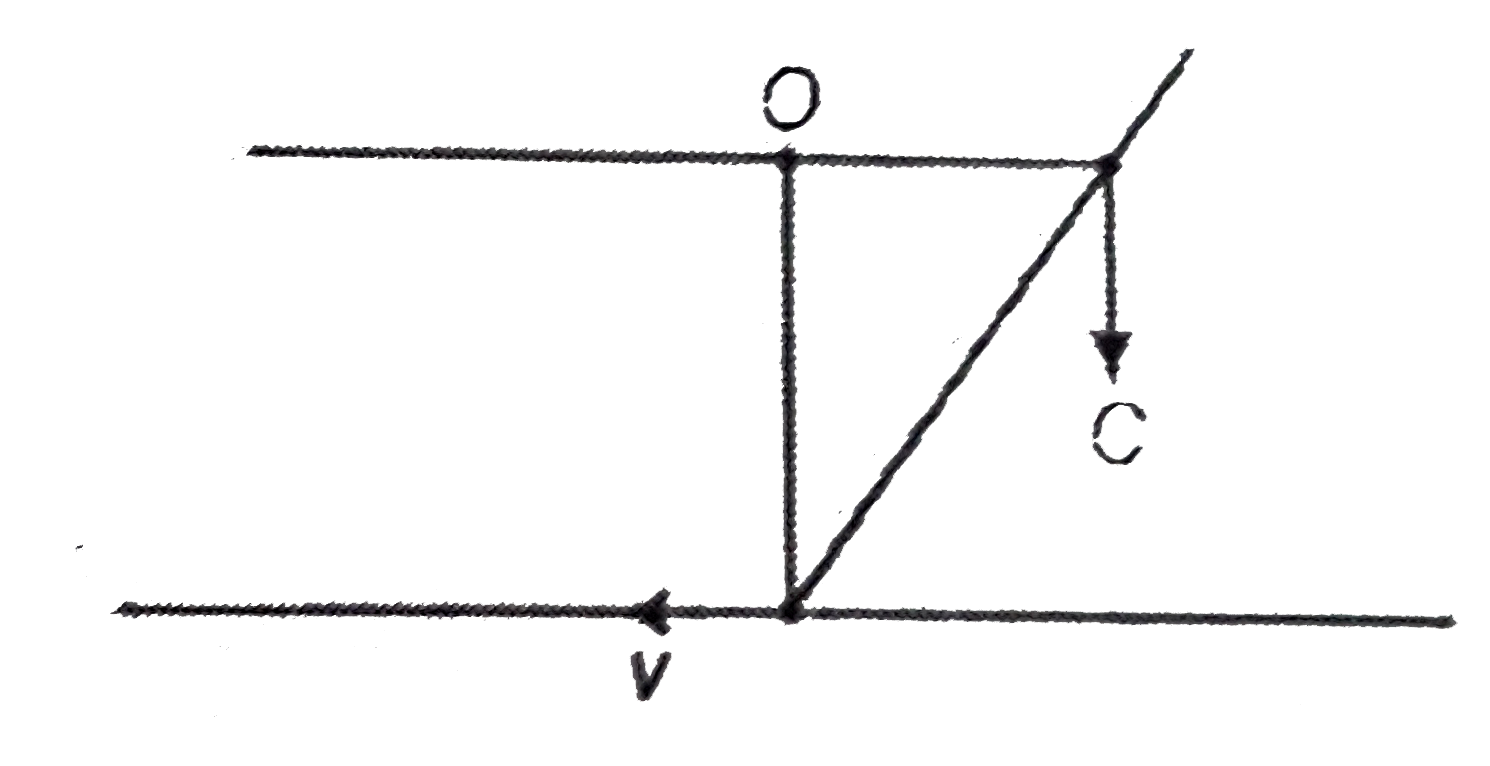
A uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
its center of mass moves vertically downwards on a straight line
Its center of mass remains in rest
the rod rotates about a vertical axis
Both a and c are correct
d) Since, no force is present in horizontal direction.
So, acceleration of center of mass in horizontal direction is zero. Hence, the center of mass of rod moves in vertically downward direction.

If perpendicualr are drawn at the velocities of center of mass and lower end. They are passing through point O. So, rod is rotating about instaneous axis passing through point O.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- SCALARS AND VECTORSBOOK - BITSAT GUIDECHAPTER - SCALARS AND VECTORSEXERCISE - All Questions
34 Videos
Similar Questions
A uniform rod of length 2a is held with one end resting on a smooth horizontal table making an angle a with the vertical. Show that when the rod is released, its angular velocity when it makes an angle θ with the vertical is given by
ω=[6g(cosα−cosθ)(1+3sin2α)]
View SolutionA uniform rod of length 2L is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
View Solution
Knowledge Check
A uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle α to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
Aω=√(3gsinα2l)Bω=√(2l3gsinα)Cω=√(gsinαl)Dω=√(lgsinα)A uniform rod of length L is placed with one end in contact with the horizontal and is then inclined at an angle α to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
Aω=√3gsinαLBω=√2L3gsinαCω=√6gsinαLDω=√LgsinαA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224
A rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionThe end 'A' of a uniform rod AB of length 'l' touches a horizontal smooth fixed surface. Initially the rod makes an angle of 30∘ with the vertical. Find the magnitude of displacement of the end B just before it touches the ground after the rod is released.
View SolutionA uniform rod of length 2a is held at inclination α with the horizontla with its lower end at a height h above a horizontal plane surface and is let fall. It rebounds elastically from the plane. If you just before the other end touches the plane the rod makes the same angle with the horizontal, find the value of h in terms of a and α.
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View Solution