A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemisphereical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the verticle centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

Step by step video & image solution for A small mass particle is projected with an initial velocity v_(0) tangent to the horizontal rim of smooth hemisphereical bowl at a radius r_(0) from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the verticle centre line, its velocity v makes an angle theta with the horizontal tangent to the bowl through B. Determine theta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE
83 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE
41 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
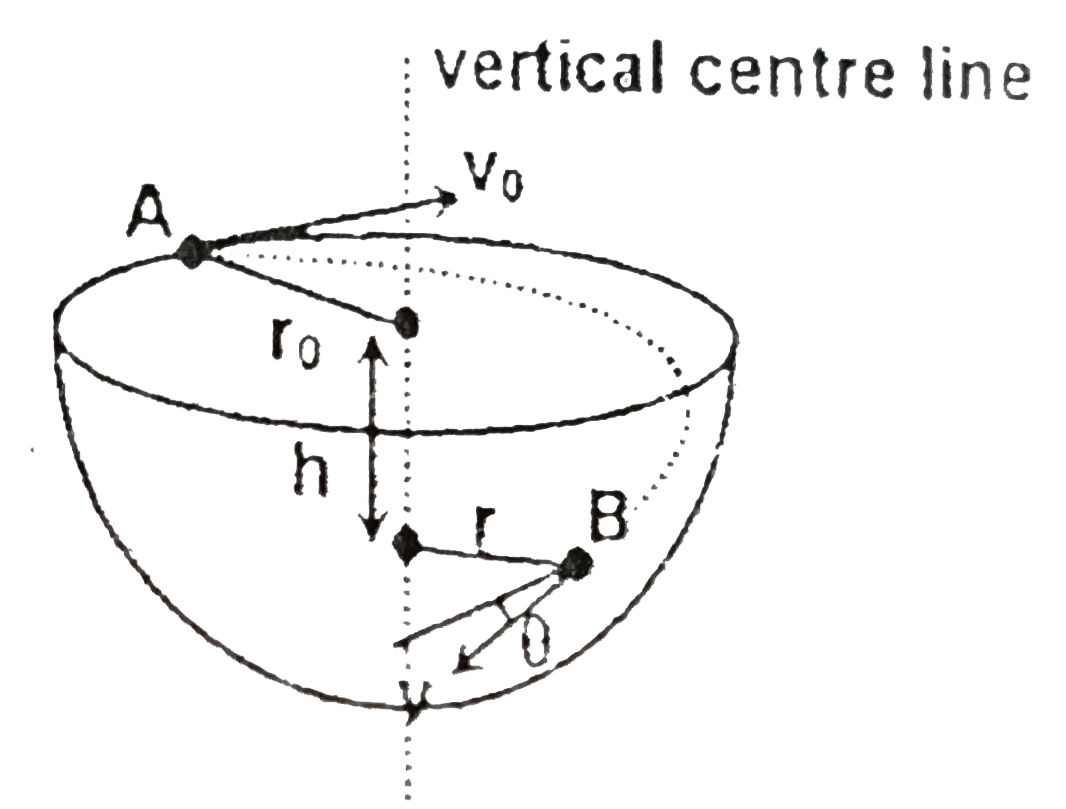
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)

View Solution
Knowledge Check
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The speed of particle at point B
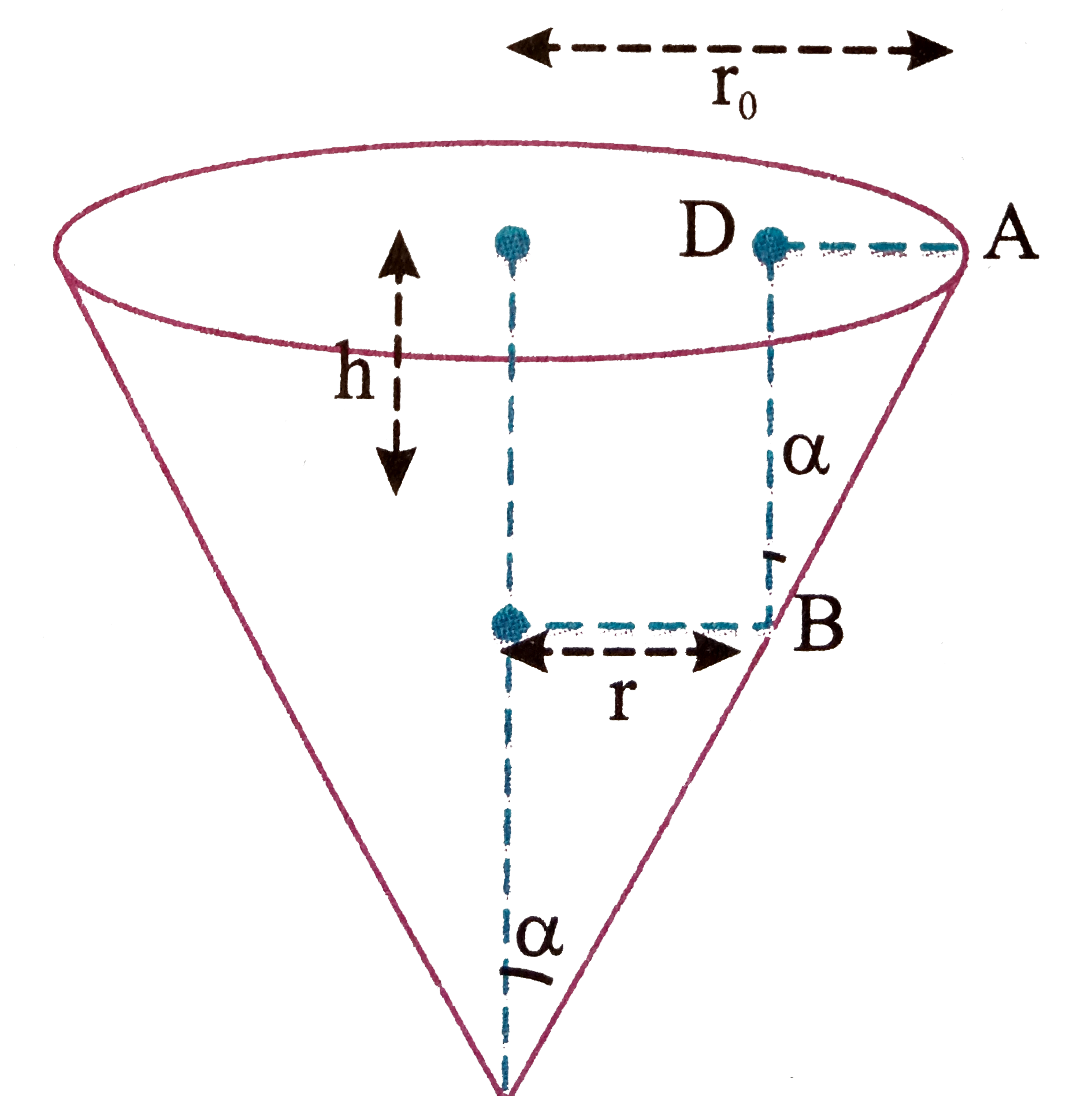 A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2gh
A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The value of θ is
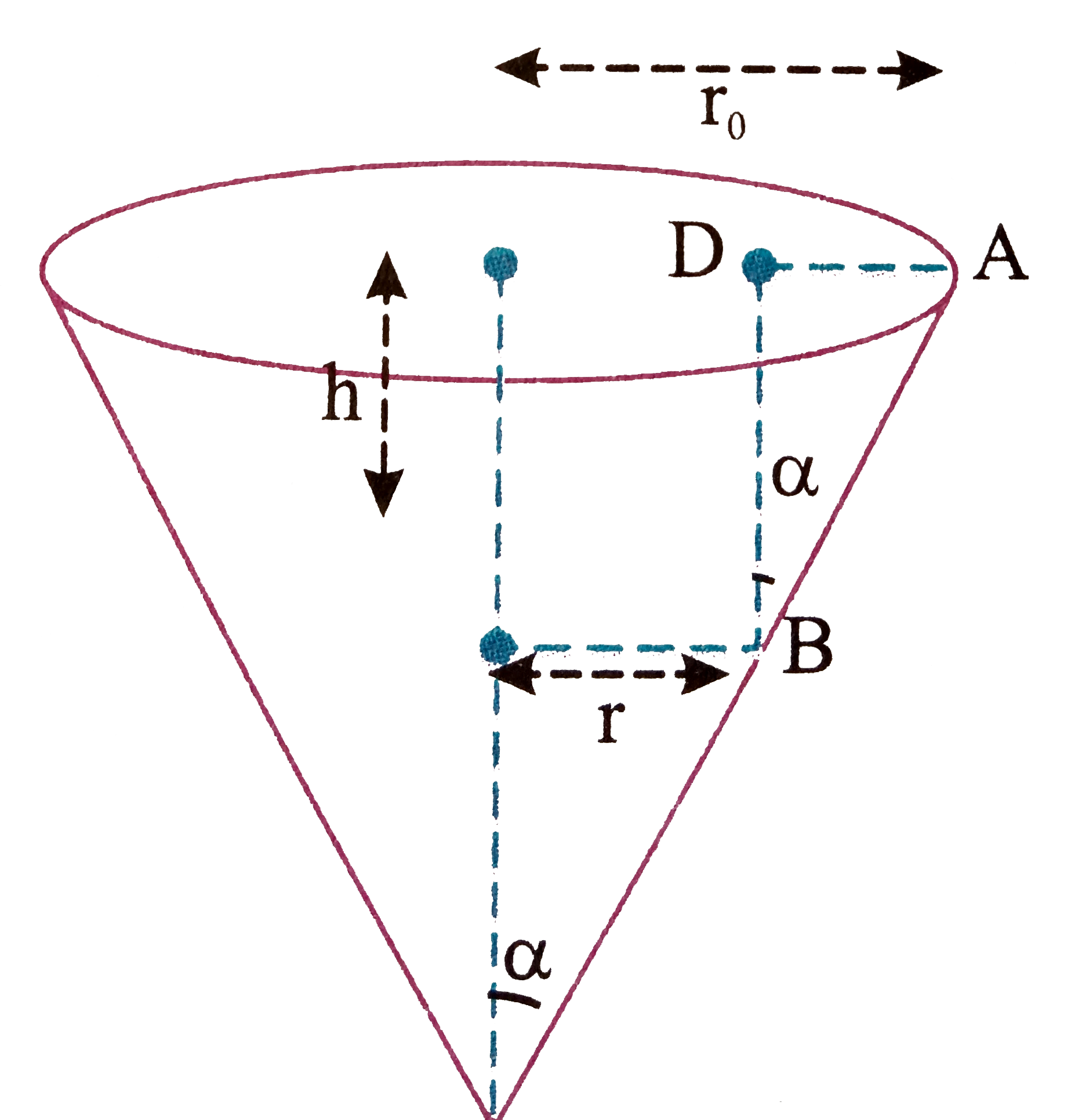 Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh
Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
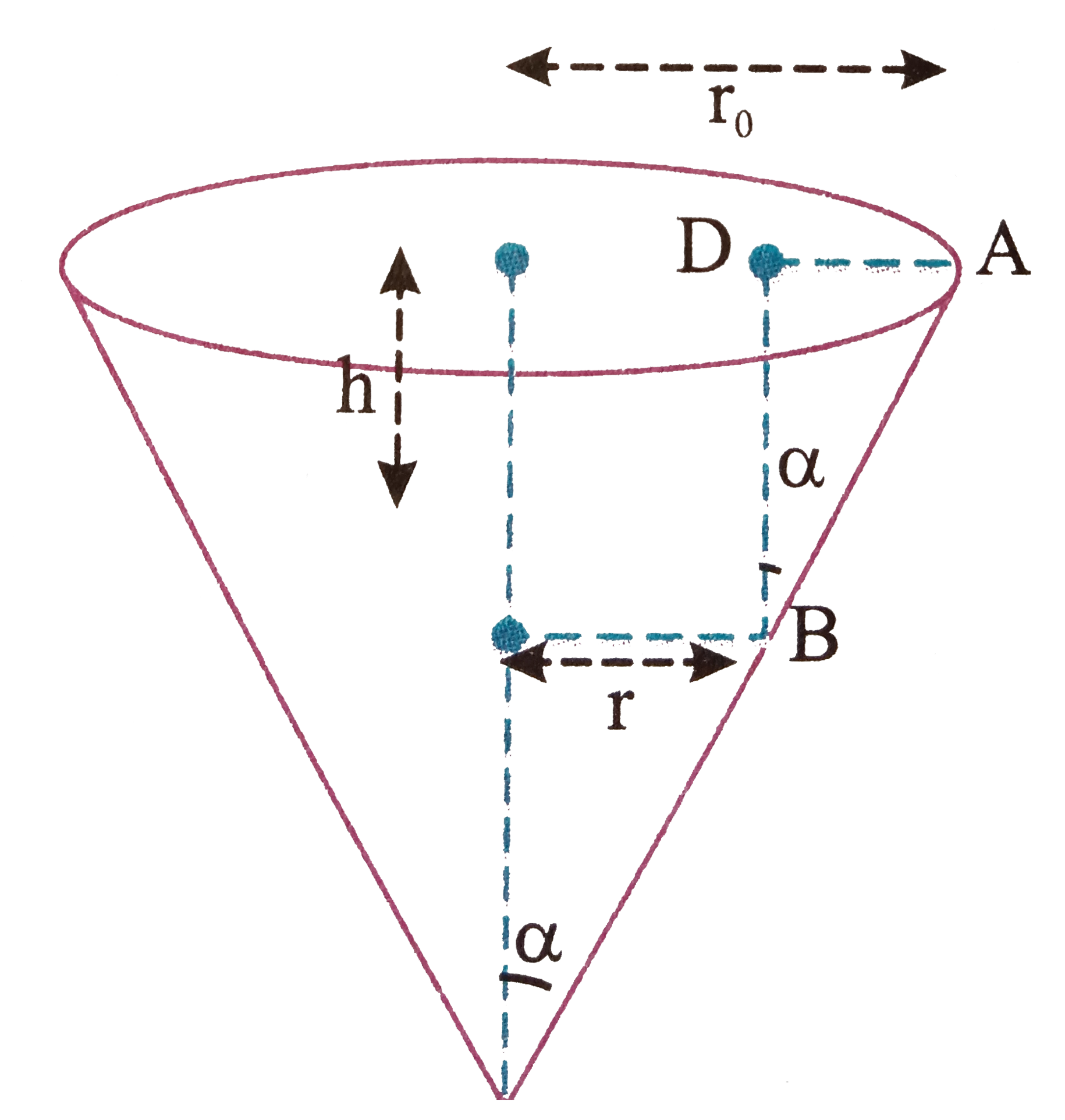 A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
View Solution
