A particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
g2sin2θu2
2g2sinθu2
g2sinθu2
g2sin2θ2u2
The correct Answer is:D
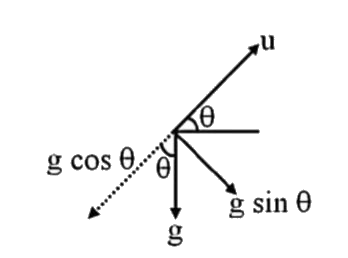
R.O.C. =u2gsinθ
at=gcosθ
so atR.O.C=gcosθu2×g
Topper's Solved these Questions
Similar Questions
Knowledge Check
A psrticle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
A(a) Varies linearly with timeB(b) Is constant throughoutC(c) Is negative for complete pathD(d) None of the aboveA projectile is thrown with a velocity u0 at an angle θ with the horizontal. The ratio of the rate of change of speed w.r.t. time, at highest point to that at the point of projection, is
AgsinθB−gsinθCzeroDg
A projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with a speed u at an angle θ with the horizontal . If R1 is radius of curvature of trajectory at the initial point and R2 is the radius of curvature at the highest point . Value of R2/(R1 is found to be cosnθ. What is the value of n ?
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View Solution

