O is a point at the bottom of a rough plane inclined at an angle α to horizontal Coefficient of friciton between AB is tanα2 and between BO is 3tanα2B is the middle point of AO, A block if released from rest at A, then which of the following graphs are correct :

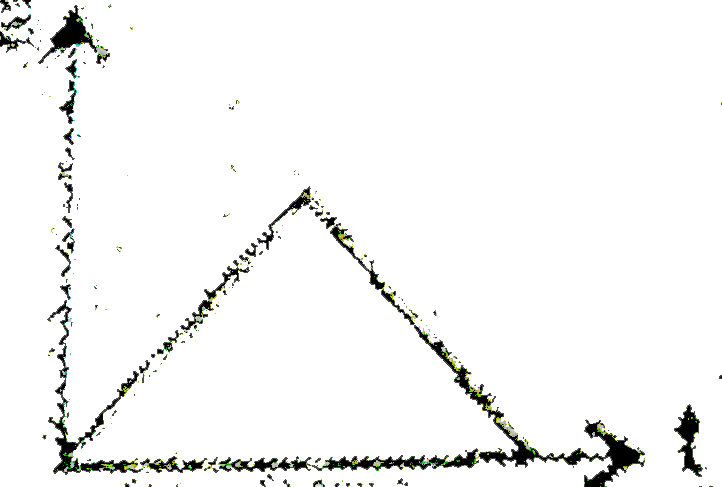
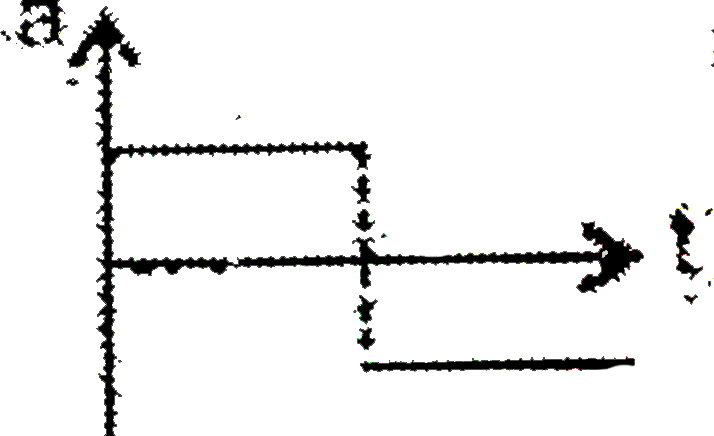
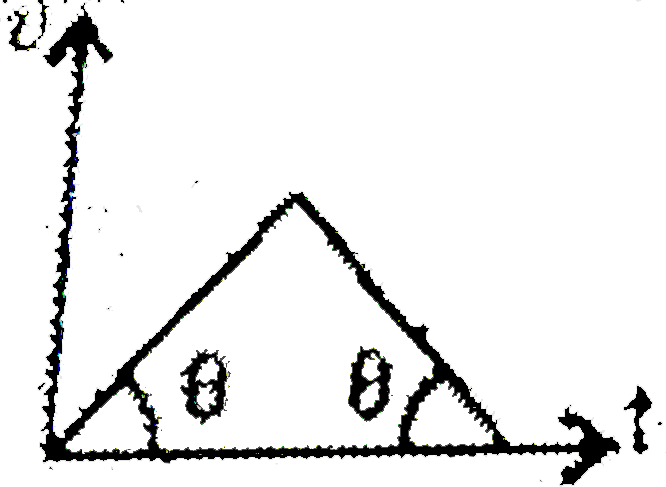

The correct Answer is:b,c
Step by step video, text & image solution for O is a point at the bottom of a rough plane inclined at an angle alpha to horizontal Coefficient of friciton between AB is (tan alpha)/(2) and between BO is (3 tan alpha)/(2)B is the middle point of AO, A block if released from rest at A, then which of the following graphs are correct : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-3
49 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - level 1
103 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
Similar Questions
Knowledge Check
O is a point at the bottom of a rough plane inclined at an angle α to the horizontal. Coefficient of friction between AB is Tanα2 and between BO is 3Tanα2 . B is the mid–point of AO. A block is released from rest at A. Then identify which graphs are correct during motion of block from point A to O taking direction down the incline plane as positive (sinα=1/5) :
 A
A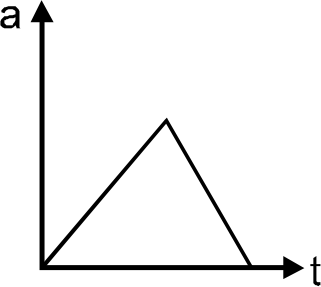 B
B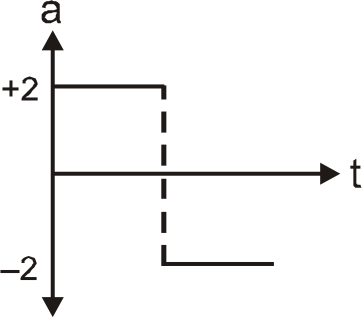 C
C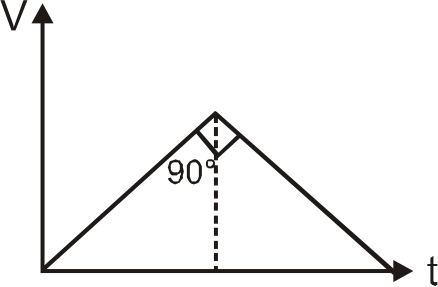 D
D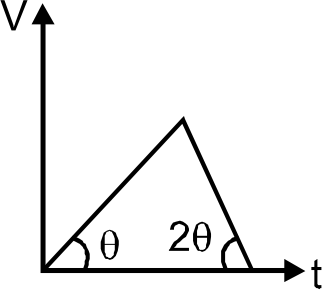
If tanα=3andtanβ=12, then which of the following is true ?
Aα+β=πc4Bαβ=πc4Cα−β=πc4DNone of theseA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of these
Consider an object P on an inclined plane of inclination β.
A shot is fired O at an angle α with horizontal. Find the relation between α and β, if the shot hits the object horizontally.

View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)

The frictional force acting between the two blocks in the previous question is :
View Solution
