Nucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
1λ1ln(2λ13λ2)
1λ1ln(8λ13λ2)
1λ1ln(7λ13λ2)
1λ1ln(4λ13λ2)
The correct Answer is:D
dNBdt=λ1NA−λ2NB
0=λ1(2N0)e−λt0−λ2(3N02),t0=1λ1ln(4λ13λ2)
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Previous JEE questions
21 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-I-(H.W)
16 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Level-V Multiple answer questions
45 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
Similar Questions
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View Solution
Knowledge Check
Nucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
At0=1λ1ln[3λ12λ2]Bt0=1λ1lm[λ1λ2]Ct0=1λ1ln[2λ13λ2]Dt0=1λ2ln[3λ12λ2]Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
ATheir number of radioactive nuclei will be equal at t=ln2λBTheir decay rate will be equals at t=ln4λCTheir decay rate will be equal at t=ln3λDAt t=ln4λ the decay rate of A will be greater than that of B.At time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
AN1N2e−(λ1+λ2)tB(N1N2)e−(λ1−λ2)tC(N1λ1e−(λ1t)+N2λ2e−λ2t)DN1λ1N2λ2e−(λ1+λ2)t
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The net rate of accumulation of B at any instant is
View SolutionA radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
View SolutionRadioactive material 'A' has decay constant '8λ' and material 'B' has decay constant 'lamda'. Initial they have same number of nuclei. After what time, the ratio of number of nuclei of material 'B' to that 'A' will be 1e ?
View SolutionRadioactive material 'A' has decay constant '8λ' and material 'B' has decay constant 'lamda'. Initial they have same number of nuclei. After what time, the ratio of number of nuclei of material 'B' to that 'A' will be 1e ?
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
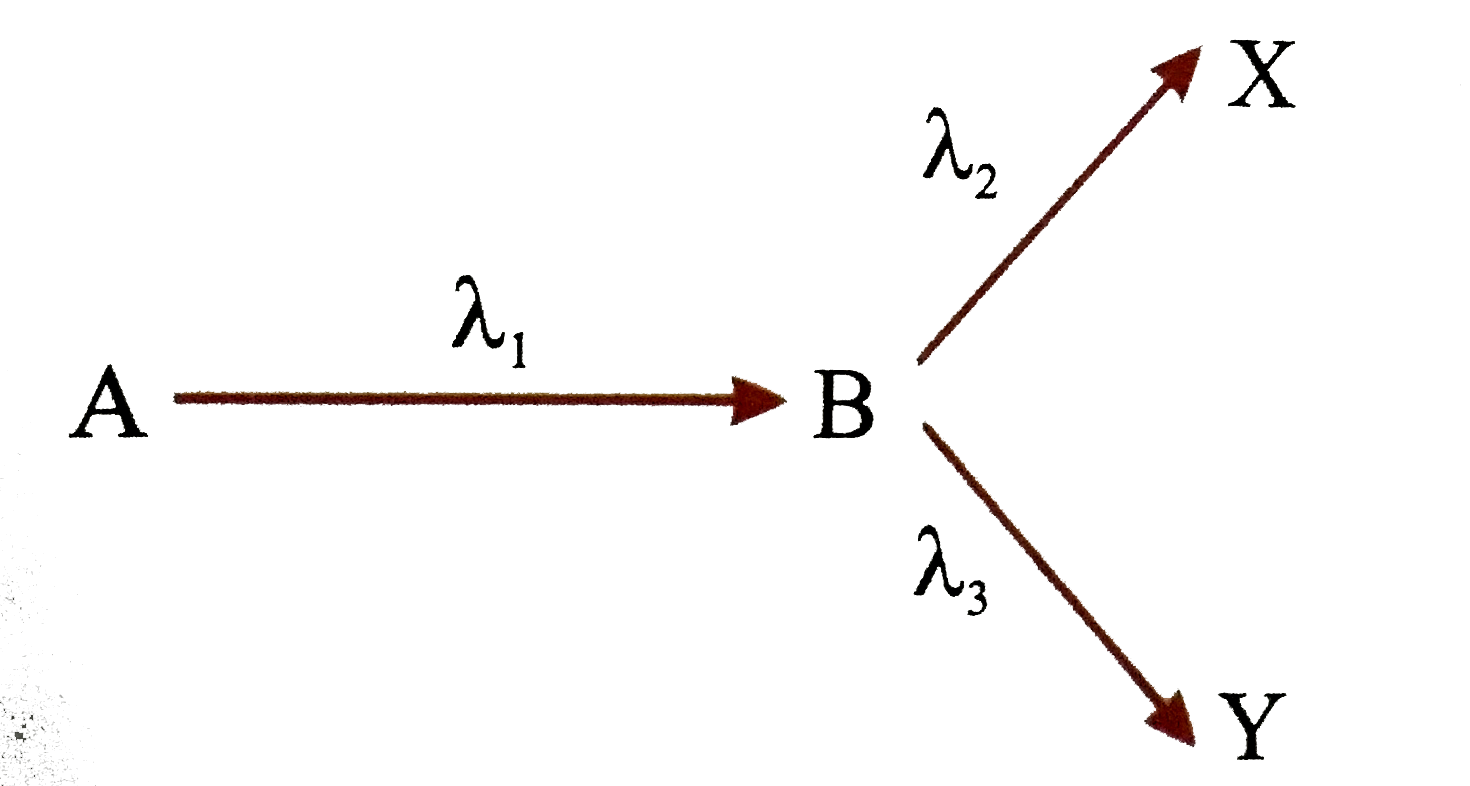
At t=∞, which of following is incorrect ?
View Solution
