An opaque sphere of radius a is just immersed in a transparent liquid as shown in figure. A point source is placed on the vertical diameter of the sphere at a distance all from the top of the sphere.One ray originating from the point source after refraction from the air liquid interface forms tangent to the sphere. The angle of refraction for that particular ray is 30∘. The refractive index of the liquid is:
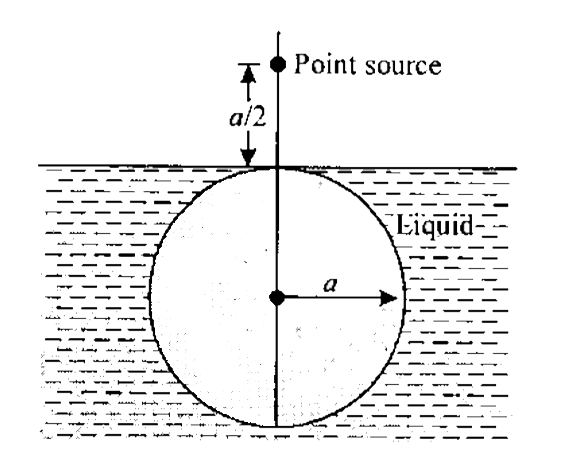
2√3
3√5
4√5
4√7
Step by step video & image solution for An opaque sphere of radius a is just immersed in a transparent liquid as shown in figure. A point source is placed on the vertical diameter of the sphere at a distance all from the top of the sphere.One ray originating from the point source after refraction from the air liquid interface forms tangent to the sphere. The angle of refraction for that particular ray is 30^(@). The refractive index of the liquid is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Advance MCQs with One or More Options Correct30videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Conceptual MCQs Single Option Correct43videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems73videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO82videos
HEAT AND THERMAL EXPANSION
Similar Questions
A light ray falls on the air glass interface at an angle of 30∘. What is the angle of refraction for this rays ? (nag=32).
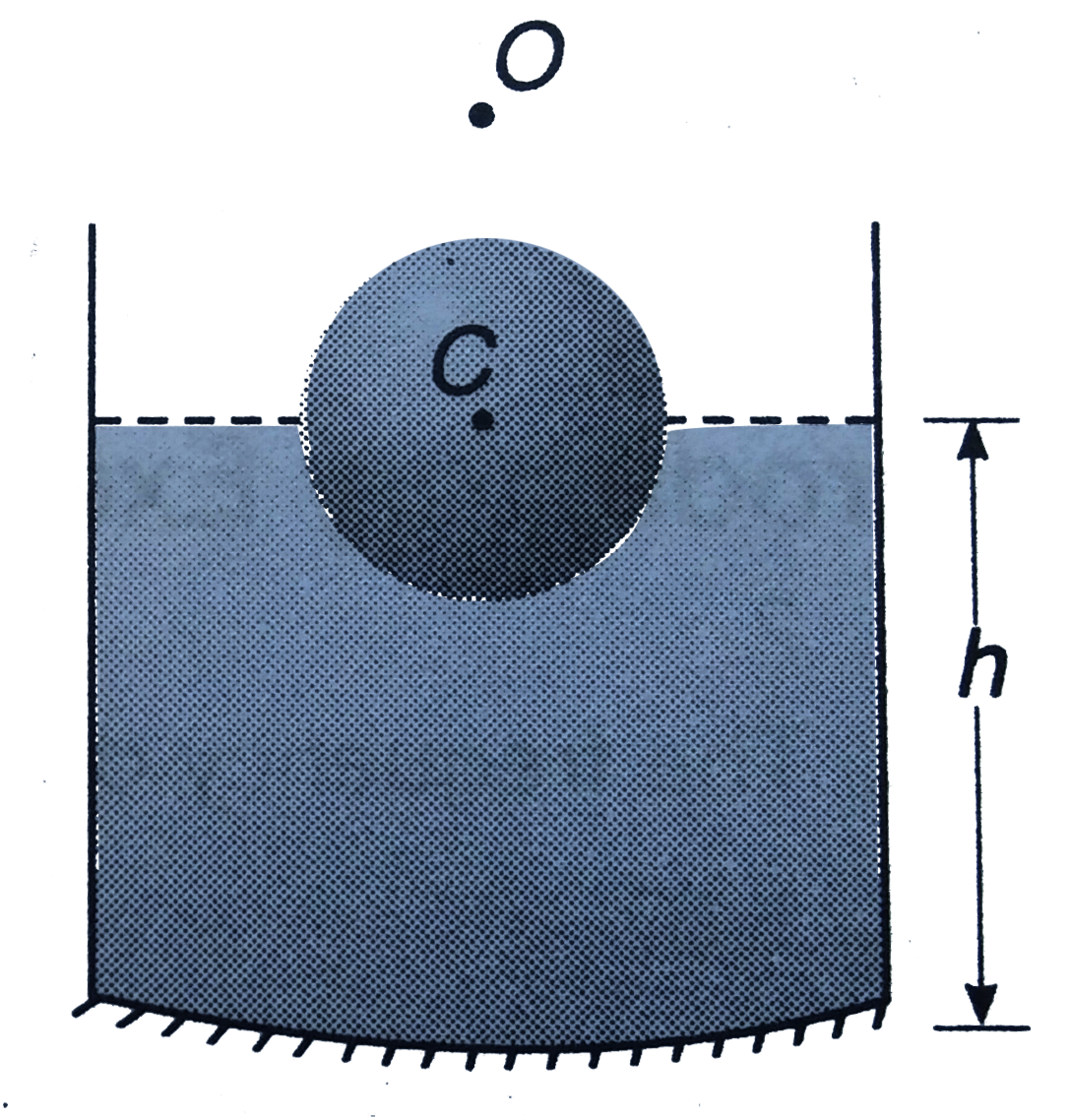
View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
A6cmB4cmC12cmD9cm - Question 2 - Select One
A ray of light passes from air into a liquid. The glancing angle is 30∘ . The deviation produced in the ray of light is 15∘. The refractive index of liquid is :
A1.224B1.268C1.339D1.52 - Question 3 - Select One
A point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
A2 cmB4 cmC6 cmD12 cm
A point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionThe minimum deviation produced by a hollow prism filled with a certain liquid is found to be 30∘. The light ray is also found to be refracted at angle of 30∘. The refractive index of the liquid is
View SolutionA point source of light is kept on the surface of a sphere and it is found that parallel light rays emerge from the other side of the sphere. What is refractive index of material of the sphere ?
View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
View SolutionThe minimum deviation produced by a hollow prism filled with certain liquid is found to be 30∘. The light ray is also found to be refracted at angle of 30∘ . The refractive index of liquid is
View Solution

