Sharp image of extended object which is placed perpendicular to the principle axis of a lens is η times that of the object for a particular position of object on a screen. Without disturbing the position of object and screen, by shifting lens a position can be obtained where the sharp image is 1/η times that of object. Ratio of difference between the two positions of lens to the focal length of lens is:
η2−1η if η>1
η2−1η if η≤1
η2−1η for all values of η
η
The correct Answer is:C
Step by step video & image solution for Sharp image of extended object which is placed perpendicular to the principle axis of a lens is eta times that of the object for a particular position of object on a screen. Without disturbing the position of object and screen, by shifting lens a position can be obtained where the sharp image is 1//eta times that of object. Ratio of difference between the two positions of lens to the focal length of lens is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Conceptual MCQs Single Option Correct
43 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
Similar Questions
a convex lens forms a virtual image of an object. What is the position of the object ?
View SolutionA 10 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. The distance of the object from the lens is 18 cm. Find the nature, position and size of the image formed.
View Solution
Knowledge Check
A 5 cm tall object is placed perpendicular to the principle axis of a convex lens of focal length 20 cm. The distance of the object from lens is 30 cm. Then, position and size of image formed is
AV= - 60 cm and h = 10 cmBV= + 60 cm and h = 10 cmCV= - 30 cm and h = 5 cmDV= + 60 cm and h = 5 cmAn object of height 5 cm is placed perpendicular to the principal axis of a concave lens of focal length 10 cm. If the distance of the object from the optical centre of the lens is 20 cm. Position, nature and size of the image formed.
A6.67 cm, -1.67 cm, real, invertedB-6.67 cm, 1.67 cm, virtual, erectC-6.67 cm, -1.67 cm, real, erectD-6.67 cm, -1.67 cm, real, invertedThe magnifications for two positions of image of the same lens are 3 and 2, of a fix point object on a fix screen when the distance between the two positions of lens is 30 cm .
The focal lengths of the lens isA180 cmB90 cmC30 cmD15 cm
A 10 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. The distance of the object from the lens is 18 cm. Find the nature, position and size of the image.
View SolutionTwo point objects A and B are kept on the principal axis of a convex lens as shown. Image of both the objects is formed at same position. Find the focal length of the lens.
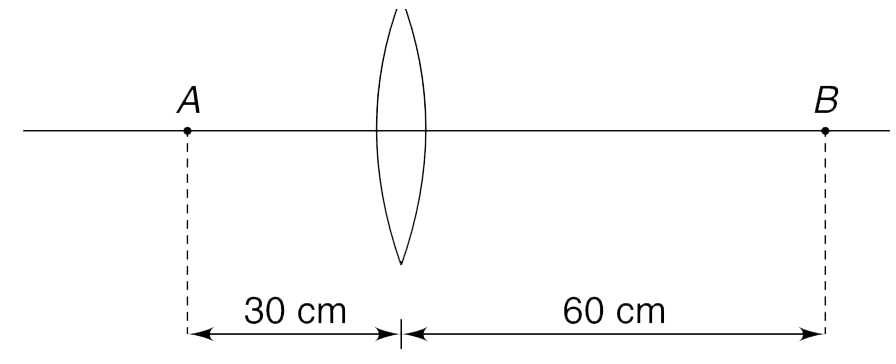
View SolutionA convex lens forms a blurred image of an object on a screen.
Suggest a suitable way to get a sharp image on a screen without disturbing the object , lens or the screen.
View SolutionAn object is placed 12cm in front of a lens to form an image on a screen. The size of the image is twice that of the object. What is the distance between the object and the image?
View SolutionIn the displacement method, a convex lens is placed in between an object and a screen if the magnification in the two position are m1 and m2(m1>m2) and the distance between the two positions of the lens is x, the focal length of the lens is
View Solution
