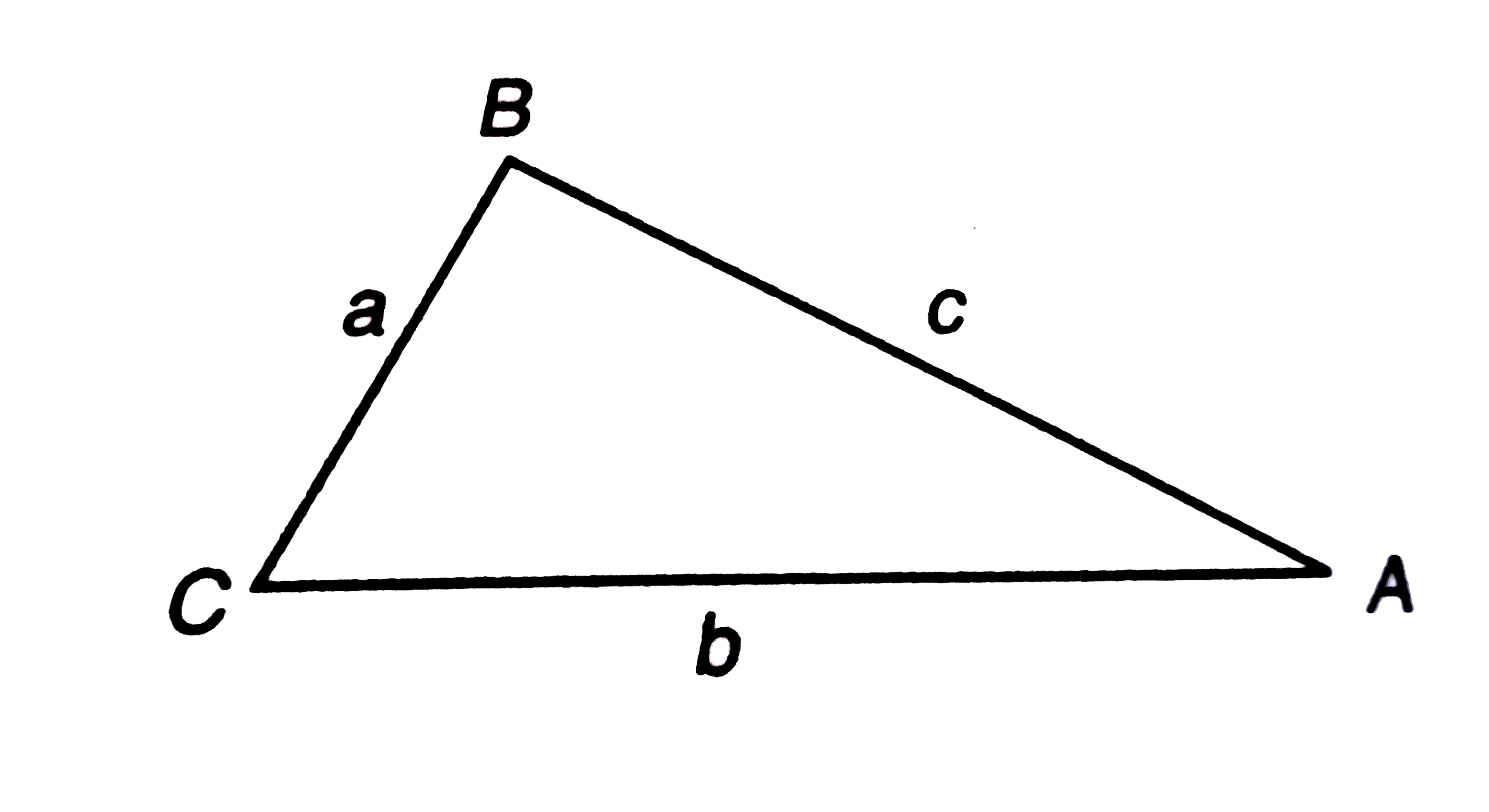
In △ABC above, a=2x, b=3x+2, c=√12, and ∠C=60∘. Find x.
A
0.50
B
0.64
C
0.77
D
1.64
Video Solution
Text Solution
The correct Answer is:B
Law of Cosines:
12=(2x)2+(3x+2)2−2⋅2x⋅(3x+2)cos60∘
12=4x2+9x2+12x+4−(12x2+8x)⋅12
7x2+8x−8=0
Use the quadratic formula to get x=±0.64
Since a side of a triangle must be positive, x can equal only 0.64.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Given the following data which, can form two triangles?
I. ∠C=30∘,c=8,b=12
II. ∠B=45∘,a=12√2,b=12√2
III. ∠C=60∘,b=12,c=5√3Aonly IBonly IIConly IIIDonly I and II
In △ABC,AB=10cm,∠A=45∘ and ∠C=60∘. Find BC.
View SolutionIn △ABC, if a2+b2+c2=ac+ab√3, then
View SolutionIn ΔABC,a=x2−1,b=2x+1,∠C=120∘, find c.
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionIf x=3+2√2, find
(x−1x)3
View SolutionIn in △ABC,∠C=105∘,∠B=45∘ and a=2 cm, then find the value of b.
View SolutionIf x=2√3+2√2 find :
1x
View Solution
