Under which conditions is xyx−y negative?
0<y<x
x<y<0
x<0<y
y<x<0
The correct Answer is:B
To determine under which conditions the expression xyx−y is negative, we need to analyze the signs of the numerator xy and the denominator x−y.
1. Identify the Expression:
We start with the expression xyx−y.
2. Determine Conditions for Negativity:
The fraction ab is negative if a and b have opposite signs. Therefore, we need to analyze the signs of xy (numerator) and x−y (denominator).
3. Analyze the Numerator xy:
- xy>0 when both x and y are either positive or both are negative.
- xy<0 when one of x or y is positive and the other is negative.
4. Analyze the Denominator x−y:
- x−y>0 when x>y.
- x−y<0 when x<y.
5. Case Analysis:
We will consider different cases based on the signs of x and y:
- Case 1: Both x>0 and y>0:
- Here, xy>0 and x−y can be either positive or negative depending on the specific values of x and y. If x>y, then the expression is positive; if x<y, it is negative.
- Case 2: Both x<0 and y<0:
- Here, xy>0 (since a negative times a negative is positive) and x−y<0 (since x<y). Thus, the expression is negative.
- Case 3: x<0 and y>0:
- Here, xy<0 (since a negative times a positive is negative) and x−y<0 (since x<y). Thus, the expression is positive.
- Case 4: x>0 and y<0:
- Here, xy<0 (since a positive times a negative is negative) and x−y>0 (since x>y). Thus, the expression is negative.
6. Conclusion:
The expression xyx−y is negative under the following conditions:
- Both x<0 and y<0 (Case 2).
- x>0 and y<0 (Case 4).
Summary:
The expression xyx−y is negative when:
- x<0 and y<0
- x>0 and y<0
We start with the expression xyx−y.
The fraction ab is negative if a and b have opposite signs. Therefore, we need to analyze the signs of xy (numerator) and x−y (denominator).
- xy>0 when both x and y are either positive or both are negative.
- xy<0 when one of x or y is positive and the other is negative.
- x−y>0 when x>y.
- x−y<0 when x<y.
We will consider different cases based on the signs of x and y:
- Here, xy>0 and x−y can be either positive or negative depending on the specific values of x and y. If x>y, then the expression is positive; if x<y, it is negative.
- Case 2: Both x<0 and y<0:
- Here, xy>0 (since a negative times a negative is positive) and x−y<0 (since x<y). Thus, the expression is negative.
- Case 3: x<0 and y>0:
- Here, xy<0 (since a negative times a positive is negative) and x−y<0 (since x<y). Thus, the expression is positive.
- Case 4: x>0 and y<0:
- Here, xy<0 (since a positive times a negative is negative) and x−y>0 (since x>y). Thus, the expression is negative.
The expression xyx−y is negative under the following conditions:
- Both x<0 and y<0 (Case 2).
- x>0 and y<0 (Case 4).
The expression xyx−y is negative when:
- x<0 and y<0
- x>0 and y<0
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Under which of the following conditions is x(x−y)y negative?
Axltylt0Byltxlt0C0ltxlt0Dxlt0lty - Question 2 - Select One
Under which climatic conditions does the laterite soil develop?
AWet tropical climateBHot and dry climateCCold temperature climateDMediterranean type of climate - Question 3 - Select One
Two elements X and Y combine to form a compound XY. Under what conditions the bond formed between them will be ionic ?
AIf the difference in electronegativities of X and Y is 1.7.BIf the difference in electronegativities of X and Y is more than 1.7.CIf the difference in electronegativities of X and Y is less than 1.7.DIf both X and Y are highly electronegative.
Under which of the following sets of conditions, △G is always negative ?
View SolutionUnder which of the conditions the process will be spontaneous?
View SolutionUnder the identical conditions of temperature, the density of a gas X is two times to that of gas Y while molecular mass of gas Y is three times that of X. Calculate the ratio of pressure of X and Y.
View Solution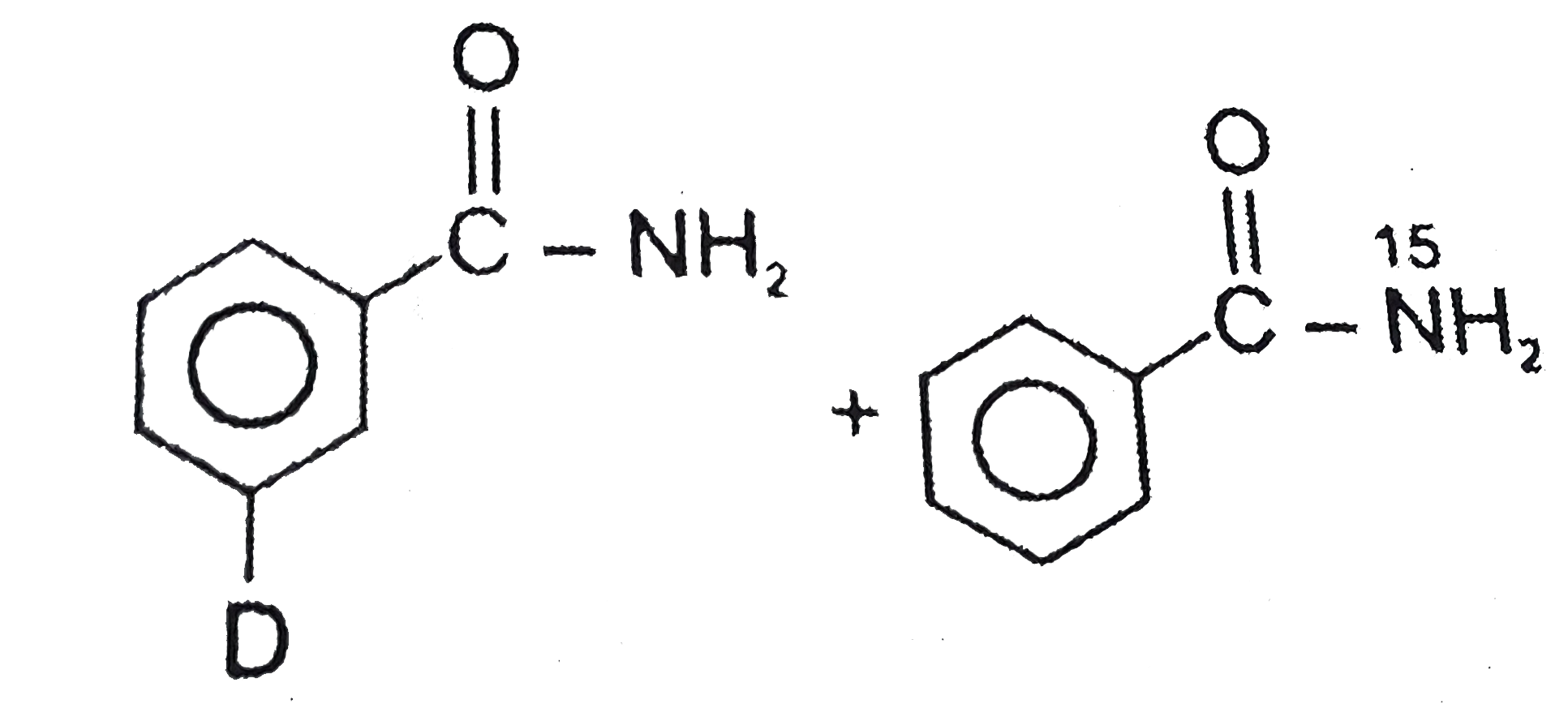 under Hofmann conditions will give:
under Hofmann conditions will give:
View SolutionUnder what condition do non-ideal solutions show negative deviations?
View Solution

