If the function k is defined by k(h)=(h+1)2, then k(k−2)=
The correct Answer is:C
To solve the problem, we need to evaluate the function k(h)=(h+1)2 at the point k−2.
1. Identify the function: We know that k(h)=(h+1)2.
2. Substitute h with k−2: We need to find k(k−2). So, we substitute h with k−2:
k(k−2)=((k−2)+1)2
3. Simplify the expression inside the parentheses:
(k−2)+1=k−1
4. Square the result:
k(k−2)=(k−1)2
5. Expand the squared term using the formula (a−b)2=a2−2ab+b2:
(k−1)2=k2−2⋅k⋅1+12=k2−2k+1
6. Final result:
k(k−2)=k2−2k+1
Final Answer:
k(k−2)=k2−2k+1
k(k−2)=((k−2)+1)2
(k−2)+1=k−1
k(k−2)=(k−1)2
(k−1)2=k2−2⋅k⋅1+12=k2−2k+1
k(k−2)=k2−2k+1
k(k−2)=k2−2k+1
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
For all real numbers x, let the function g be defined by g(x)=p(x−h)2+k, wher p, h and k are constants with p,k>0. Which of the following CANNOT be true?
Ag(7)=−hBg(7)=2Cg(0)=−2Dg(0)=2 - Question 2 - Select One
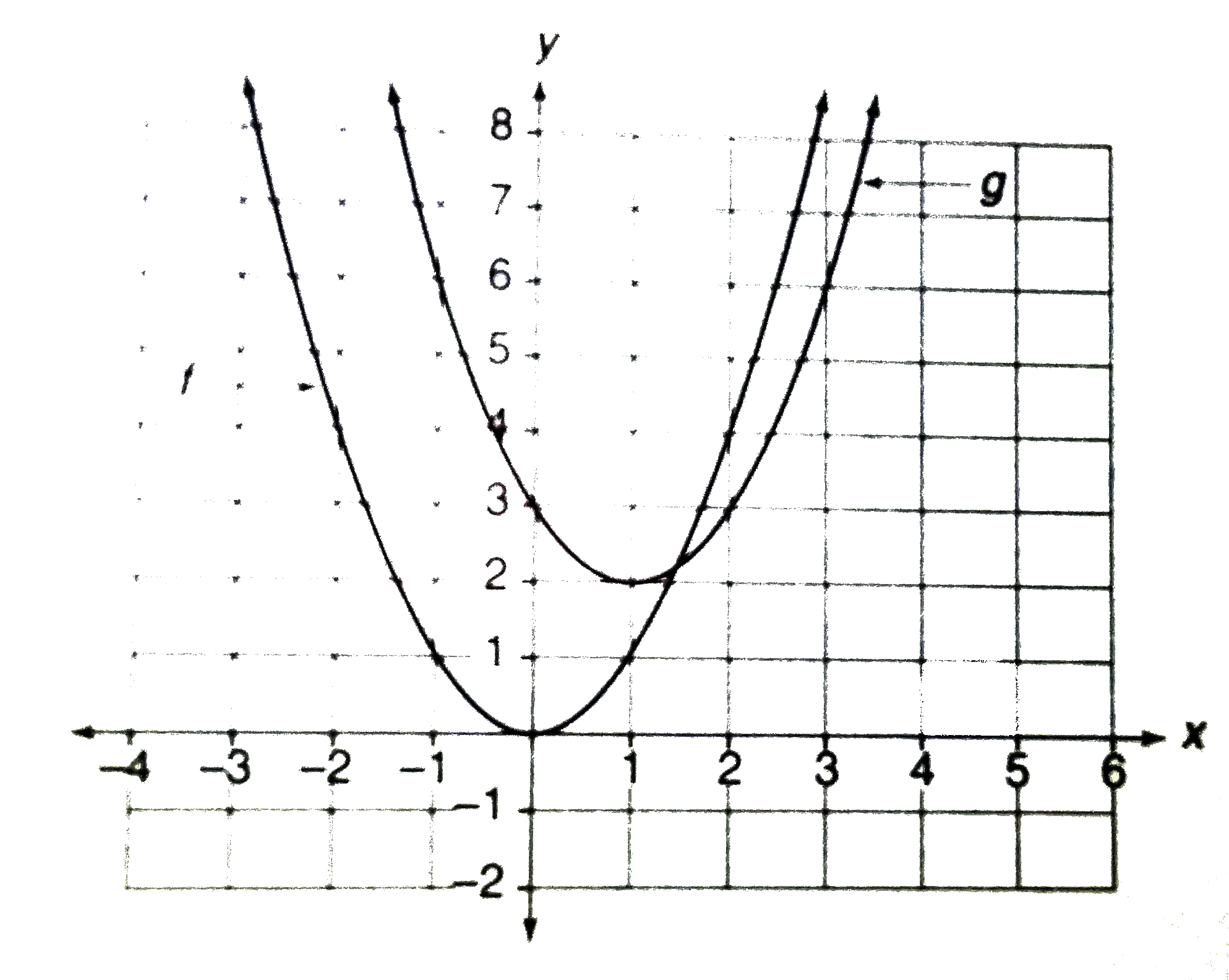
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?A−3B−2C−1D1 - Question 3 - Select One
If (k+1k)2=16, then k2+1k2=
A4B8C12D14
Find the least value of k for which the function x2+kx+1 is an increasing function in the interval (1,2)
View SolutionThe standard potential of the reaction
H2O+e−→(12)H2+OH− at 298 K by using kw(H2O)=10−14, is:View SolutionProve that the straight lines joining the origin to the point of intersection of the straight line hx+ky=2hk and the curve (x−k)2+(y−h)2=c2 are perpendicular to each other if h2+k2=c2.
View SolutionIf h is even, j is odd, and k is odd, what is k(h+j)?
View Solution
The graphs above show the complete functions h and k. which one of the following expresses k(x) in terms of h(x)?View Solution

