To find the area of parallelgram ABCD, draw perpendicular segment, BH, as shown. Since BH is the side opposite a angle in a right triangle.
The correct Answer is:
To find the area of parallelogram ABCD, we will follow these steps:
Step 1: Identify the height and base of the parallelogram.
We have a perpendicular segment BH drawn from point B to line AD. This segment represents the height (H) of the parallelogram. The base (B) of the parallelogram can be considered as the length of side AD (or BC, since opposite sides of a parallelogram are equal).
Step 2: Determine the height using the sine function.
In triangle ABH, we know that angle ABH is 45 degrees. The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. Therefore, we can write:
sin(45∘)=HHypotenuse
Given that the hypotenuse (AB) is 6 units, we have:
sin(45∘)=H6
Since sin(45∘)=1√2, we can set up the equation:
1√2=H6
Step 3: Solve for the height (H).
To find H, we can rearrange the equation:
H=6⋅1√2=6√2
We can simplify this further by multiplying the numerator and denominator by √2:
H=6√22=3√2
Step 4: Identify the base of the parallelogram.
The base AD (or BC) is given as 8 units.
Step 5: Calculate the area of the parallelogram.
The area (A) of a parallelogram is given by the formula:
A=Base×Height
Substituting the values we have:
A=8×3√2=24√2
Conclusion:
The area of parallelogram ABCD is 24√2 square units.
---
We have a perpendicular segment BH drawn from point B to line AD. This segment represents the height (H) of the parallelogram. The base (B) of the parallelogram can be considered as the length of side AD (or BC, since opposite sides of a parallelogram are equal).
In triangle ABH, we know that angle ABH is 45 degrees. The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. Therefore, we can write:
To find H, we can rearrange the equation:
The base AD (or BC) is given as 8 units.
The area (A) of a parallelogram is given by the formula:
The area of parallelogram ABCD is 24√2 square units.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
To Find the area of △JKL, drop a perpendicular segment from vertex J to side KL, extending it as necessary. Since △JKH measures 30∘:

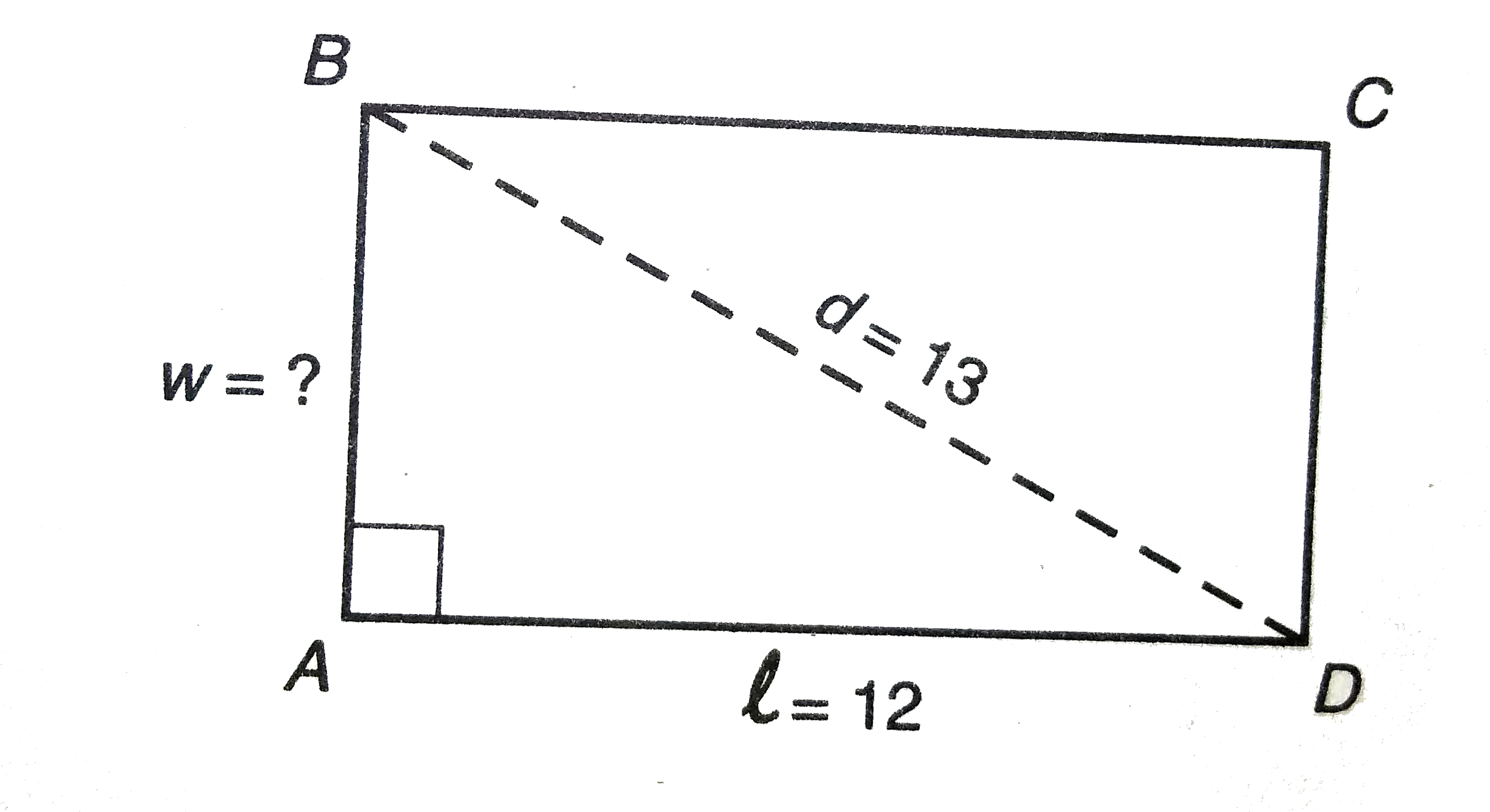
View SolutionTo find the area of rectangle ABCD, note that the diagonal form a (5−12−13) right triangle so the width of the rectangle is 5. Hence,Find area of triangle.:
View SolutionIf the area(!) and an angle(θ) of a triangle are given , when the side opposite to the given angle is minimum , then the length of the remaining two sides are
View SolutionProve that If the bisector of any angle of a triangle and the perpendicular bisector of its opposite side intersect, they will intersect on the circumcircle of the triangle.
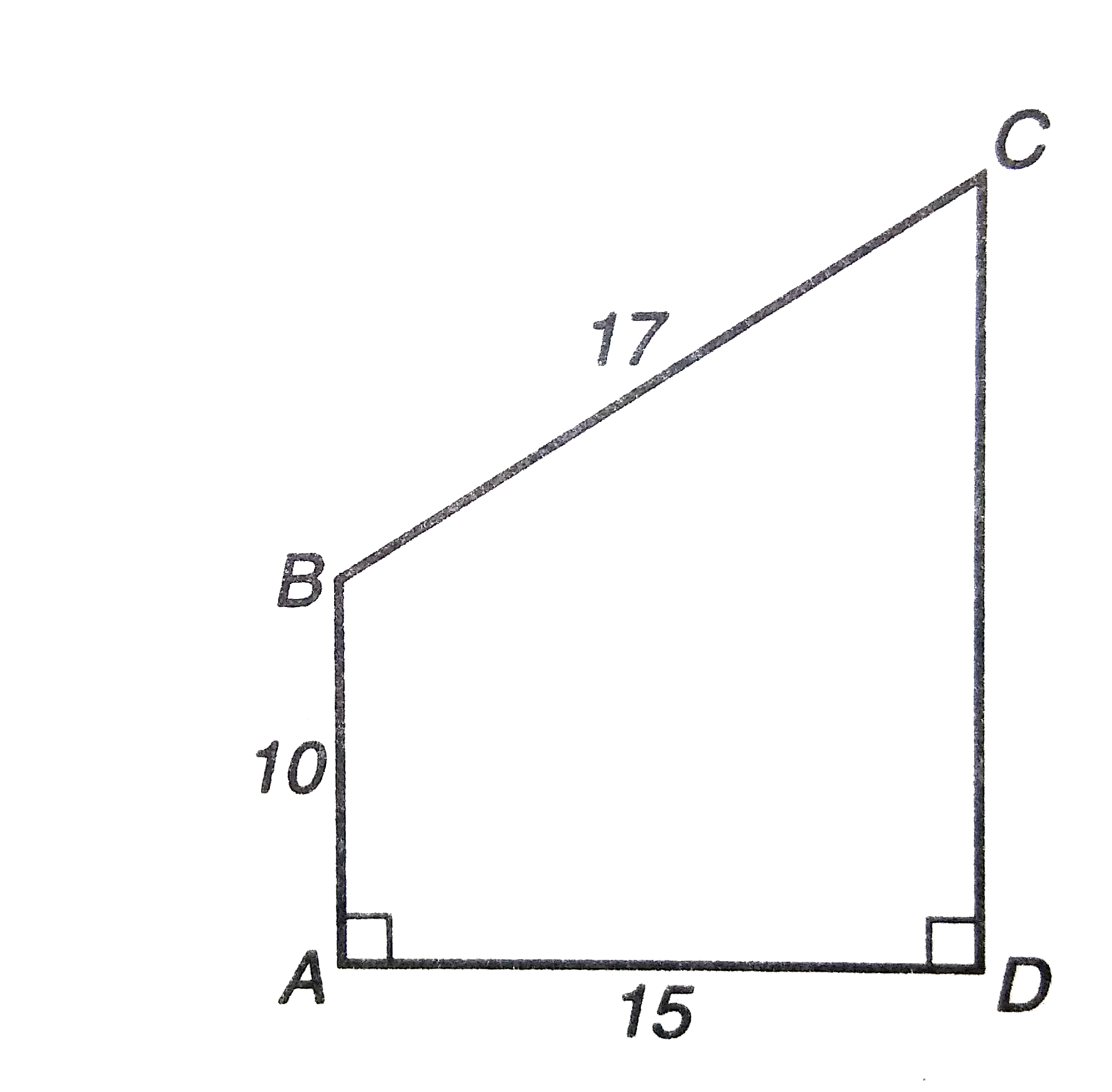
View SolutionTo find the area of trapezoid ABCD, first the length of base CD by drawing heigth BH to CD. Since parallel lines are everywhere equidistant, BH=AD=15. The lengths of the sides of right triangle BHC from an (8-15-17) Pythagorean triple, where CH=8. Thus, CD=CH+HD=8+10=18.
View SolutionThe area of a right-angled triangle is 54 sg. cm. If one of the two perpendicular sides is 9 cm, find the other.
View SolutionIf the square of one side of a triangle is equal to the sum of the squares of the other two sides then the triangle is a right triangle with the angle opposite the first sides as right angle.
View SolutionFind the area of the right-angled triangle with hypotenuse 40 cm and one of the other two sides 24 cm.
View SolutionProve that in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angles opposite to the first side is a right angle.
View SolutionProve that in a triangle if the square of one side is equal to the sum of the squares of the other two side then the angle opposite to the first side is a right angle.
View Solution
