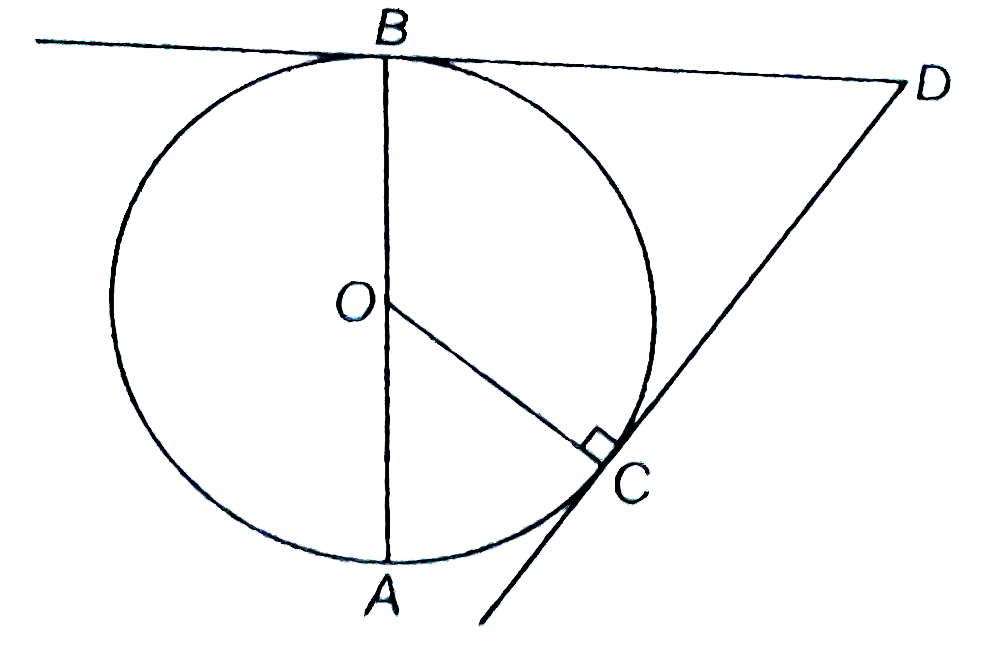
In circle O above, AB=3andCD=2. Which of the following statements must be true?
I. ∠ABCand∠BCD have equal measures
II. ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD
III. 2(AE)=3(CE)
I and II
I and III
I only
III only
The correct Answer is:D
To solve the problem, we need to analyze the statements given in the context of the circle and the segments AB and CD.
1. Understanding the Circle and Segments:
- We have a circle with center O.
- The segments AB and CD are given lengths: AB = 3 and CD = 2.
2. Analyzing Statement I:
- Statement I claims that angles ∠ABC and ∠BCD have equal measures.
- These angles intercept the same arc BD. By the property of angles in a circle that intercept the same arc, we can conclude that ∠ABC = ∠BCD.
- Therefore, Statement I is True.
3. Analyzing Statement II:
- Statement II claims that segments AB and CD are parallel (AB || CD).
- There is no information provided in the problem that indicates AB and CD are parallel. Thus, we cannot assume this to be true.
- Therefore, Statement II is False.
4. Analyzing Statement III:
- Statement III claims that 2(AE) = 3(CE).
- To analyze this, we can use the property of similar triangles.
- By the angle-angle similarity criterion, triangles ABE and CDE are similar because they share angles and have equal angles from the intercepted arcs.
- From the similarity of triangles, we have:
AECE=ABCD
Substituting the known values:
AECE=32
- Cross-multiplying gives us:
2(AE)=3(CE)
- Therefore, Statement III is True.
5. Conclusion:
- The only statements that must be true are I and III.
- Thus, the correct answer is that statements I and III are true.
Final Answer:
- Statements I and III are true.
- We have a circle with center O.
- The segments AB and CD are given lengths: AB = 3 and CD = 2.
- Statement I claims that angles ∠ABC and ∠BCD have equal measures.
- These angles intercept the same arc BD. By the property of angles in a circle that intercept the same arc, we can conclude that ∠ABC = ∠BCD.
- Therefore, Statement I is True.
- Statement II claims that segments AB and CD are parallel (AB || CD).
- There is no information provided in the problem that indicates AB and CD are parallel. Thus, we cannot assume this to be true.
- Therefore, Statement II is False.
- Statement III claims that 2(AE) = 3(CE).
- To analyze this, we can use the property of similar triangles.
- By the angle-angle similarity criterion, triangles ABE and CDE are similar because they share angles and have equal angles from the intercepted arcs.
- From the similarity of triangles, we have:
AECE=ABCD
Substituting the known values:
AECE=32
- Cross-multiplying gives us:
2(AE)=3(CE)
- Therefore, Statement III is True.
- The only statements that must be true are I and III.
- Thus, the correct answer is that statements I and III are true.
- Statements I and III are true.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
Knowledge Check
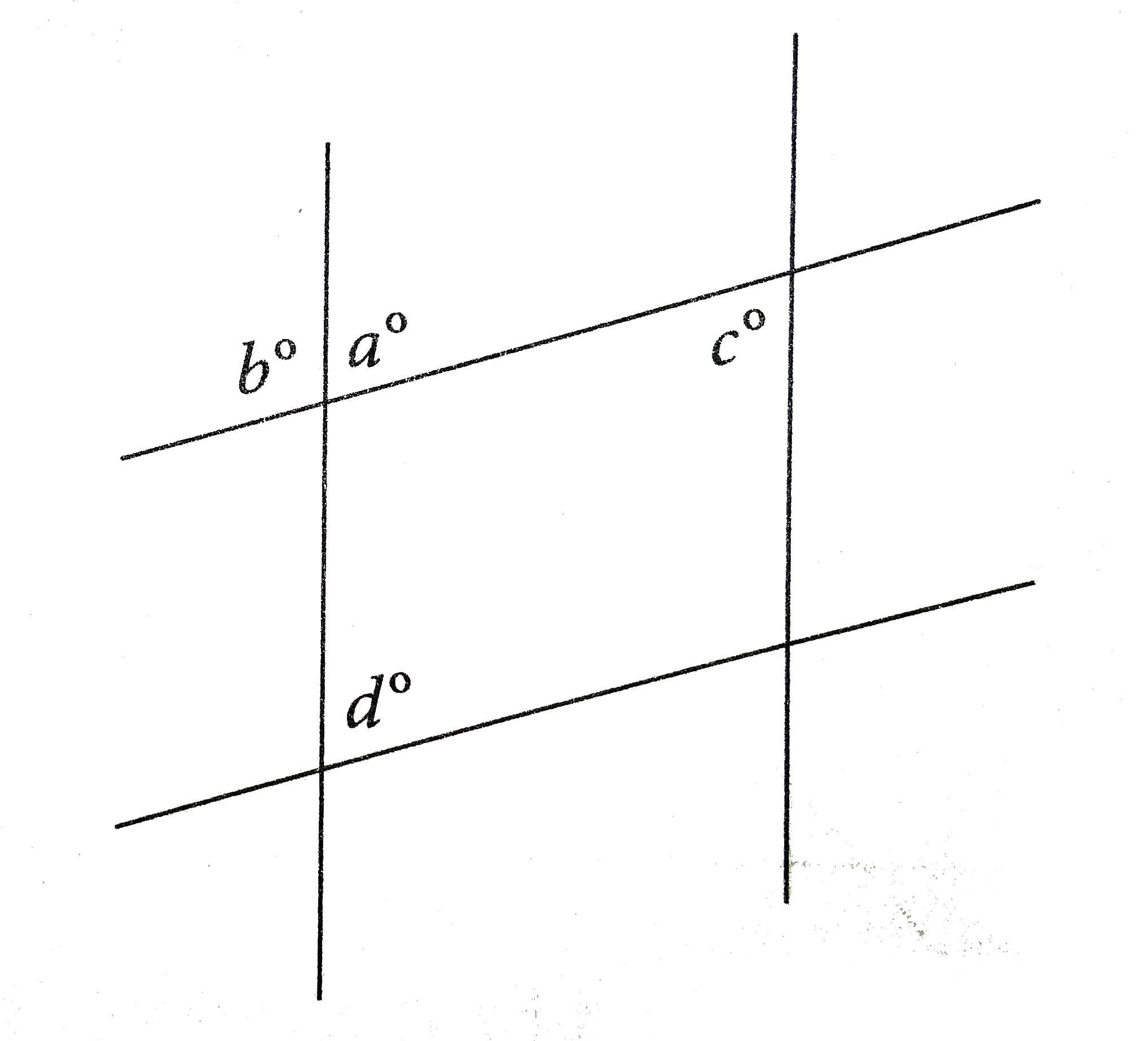
Which of the following statements must be true?
I. a+b<180
II. a+d=180
III.a+d>180ANoneBII onlyCI and II onlyDII and III only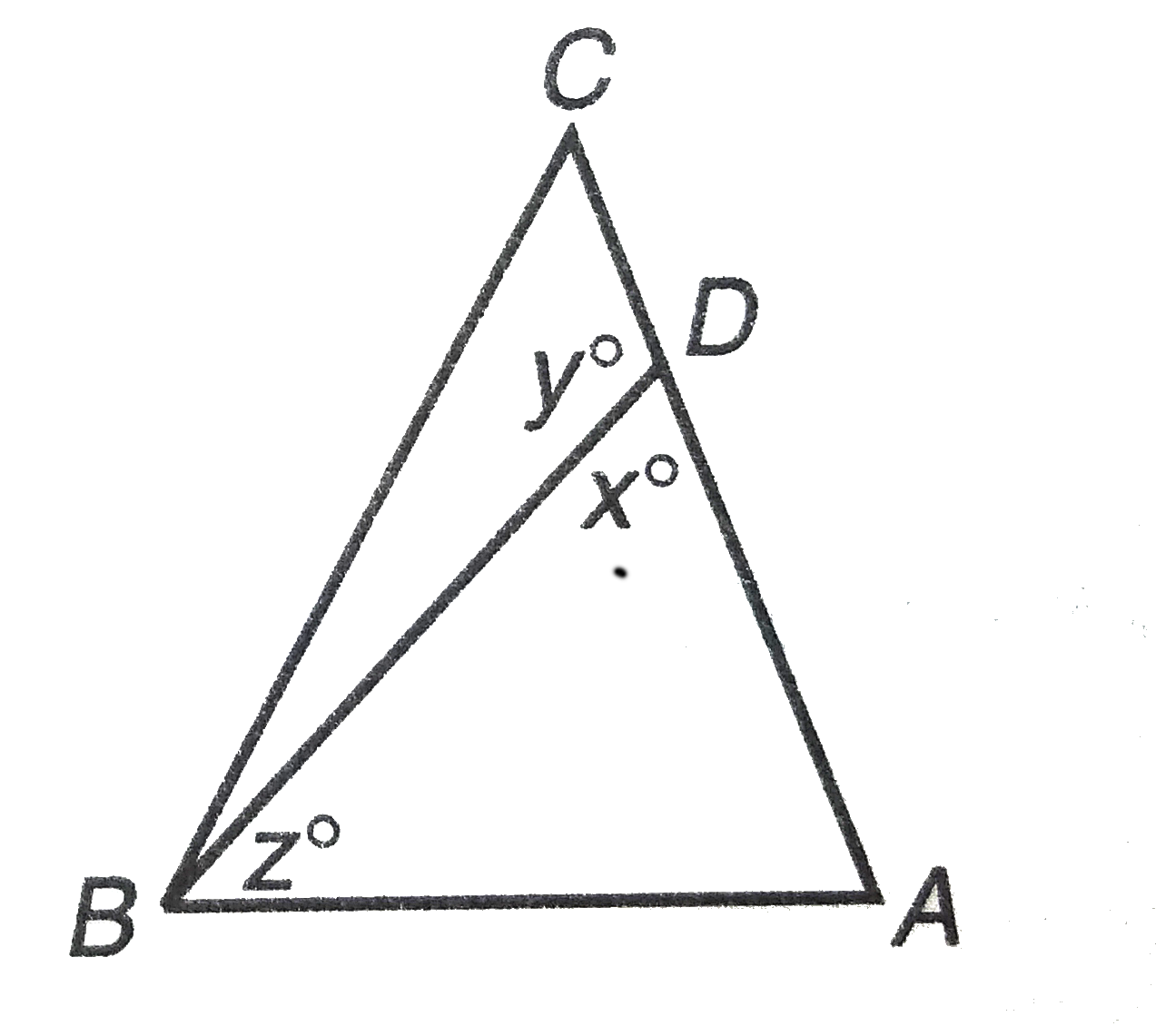
In △ABC, if AB=CD, which of the following statements must be true?
I.x>z
II. y>x
III. AB>BCAI onlyBII onlyCI and II onlyDII and III only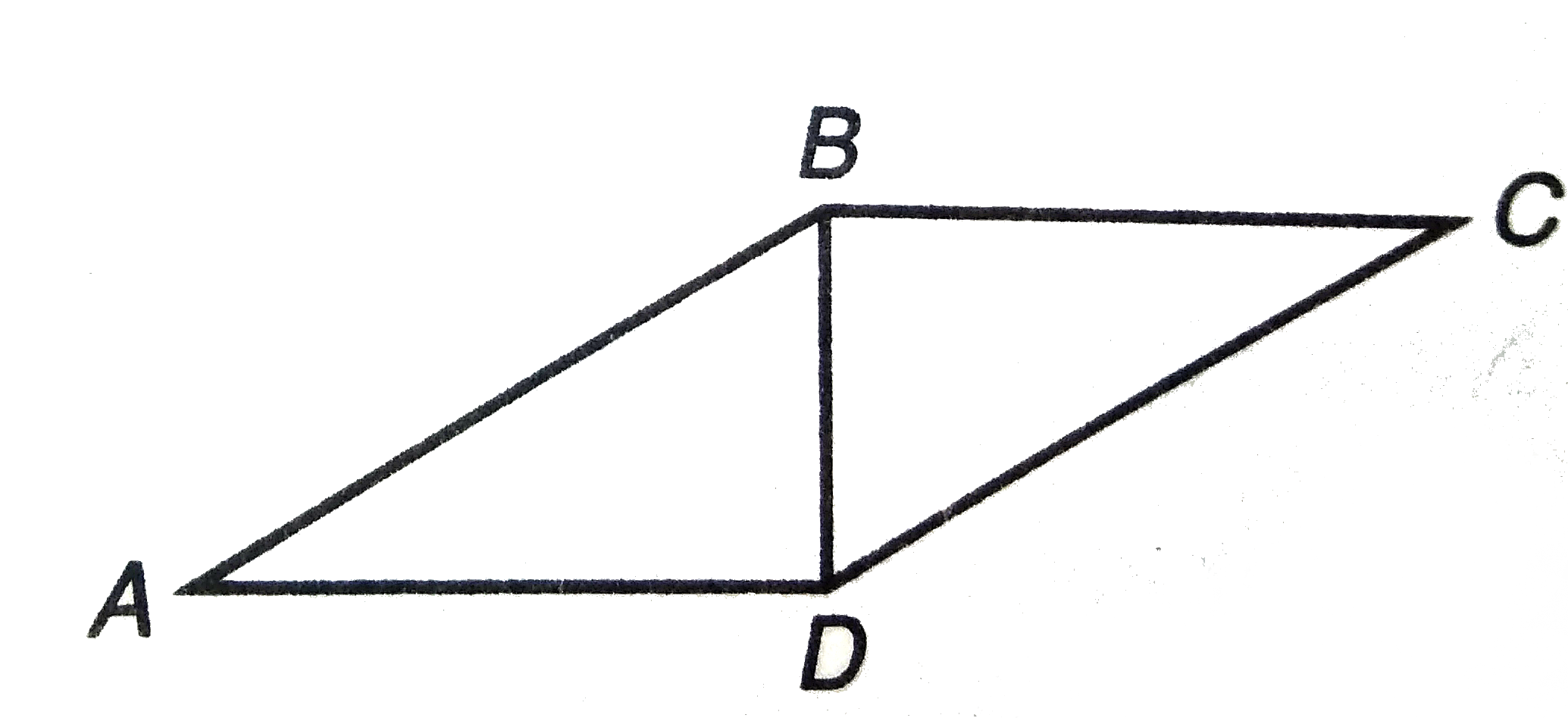
For parallelogram ABCD above, if AB>BD which of the following statements must be true?
I. CD>BD
II. ∠ADB>∠C
∠CBD>∠AANoneBI onlyCII and III onlyDI and III only
For the reaction shown below, which statement is true ?
2Fe+3CdCl2⇔2FeCl3+3Cd
View SolutionIf a=3+b, which of the following must be true?
I. a>b+2.5
II. a<b+2.5
III. a>2+b
View Solution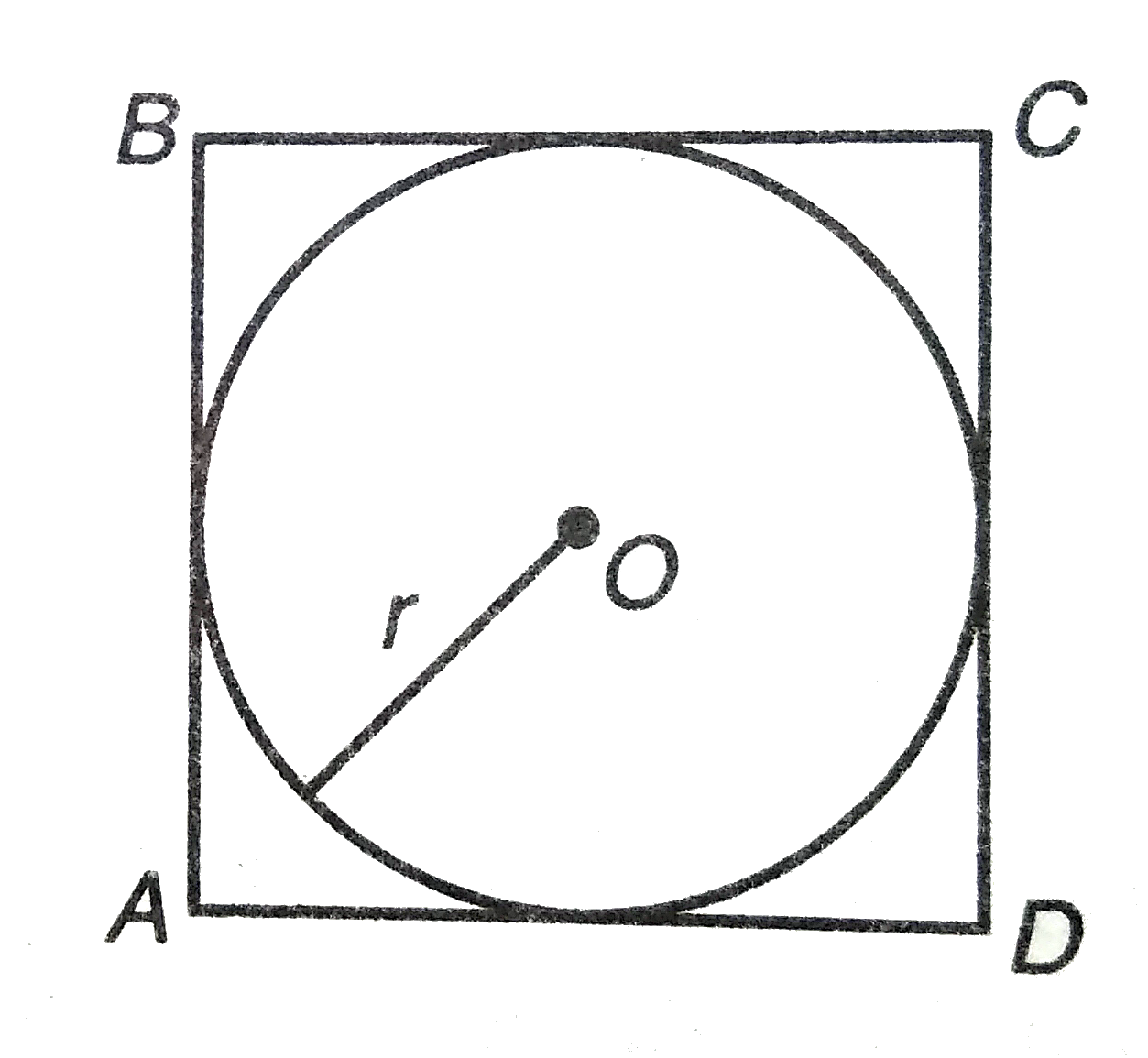
In the figure above, if circle O is inscribed in square ABCD in such a way that each side of the square is tangent to the circle, which of the following statements must be true?
I. AB×CD<π×⋊r
II. Area ABCD=4r2
III. r<2(CD)π
View Solution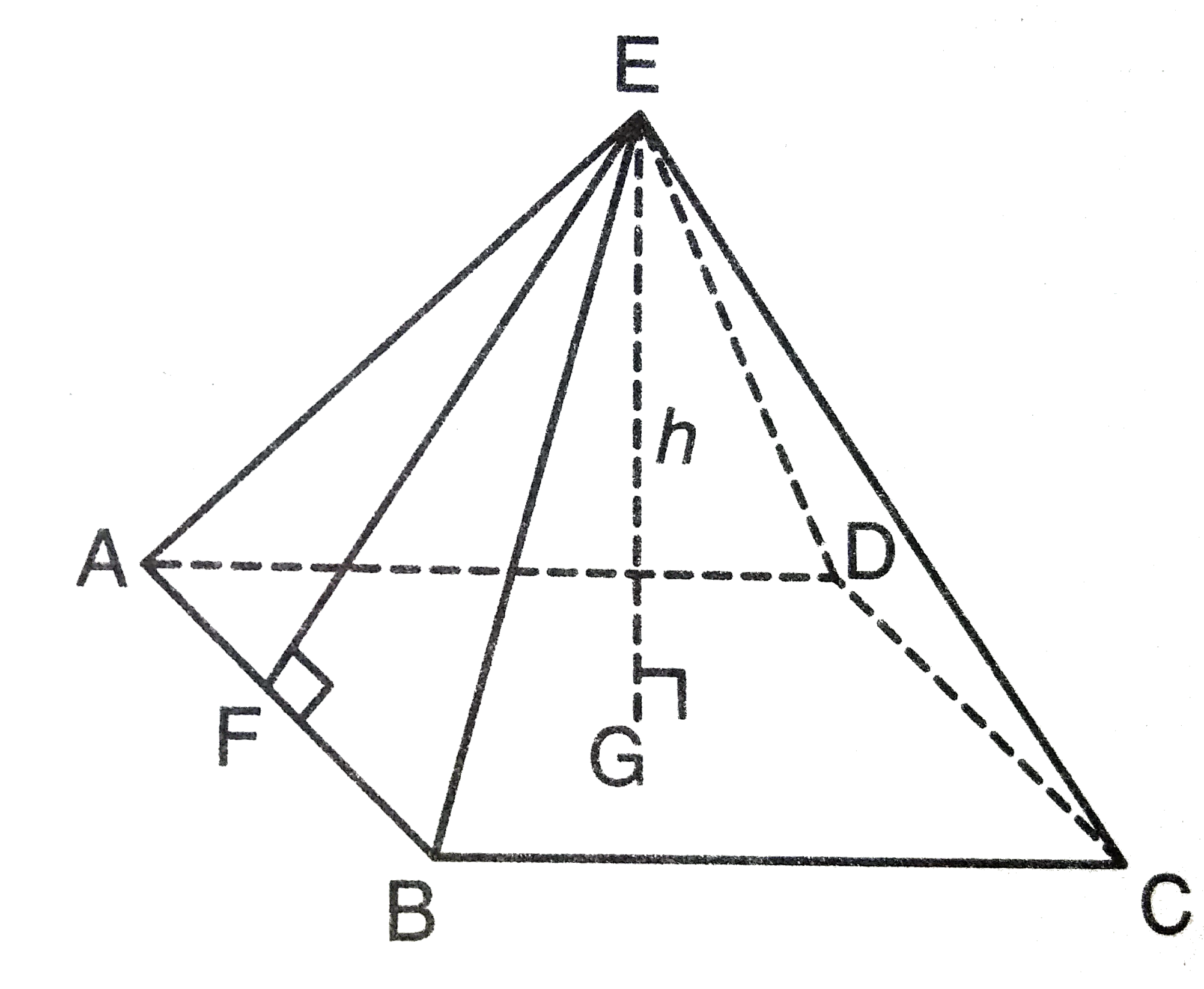
In the pyramid shown in the diagram above G is the certer of square base ABCD, ¯¯¯¯¯¯EF⊥¯¯¯¯¯¯AB and h height of the pyramid. Which statements must be true?
I. EA=EC
II. △BFC is isosceles
III. EF=EG
View Solution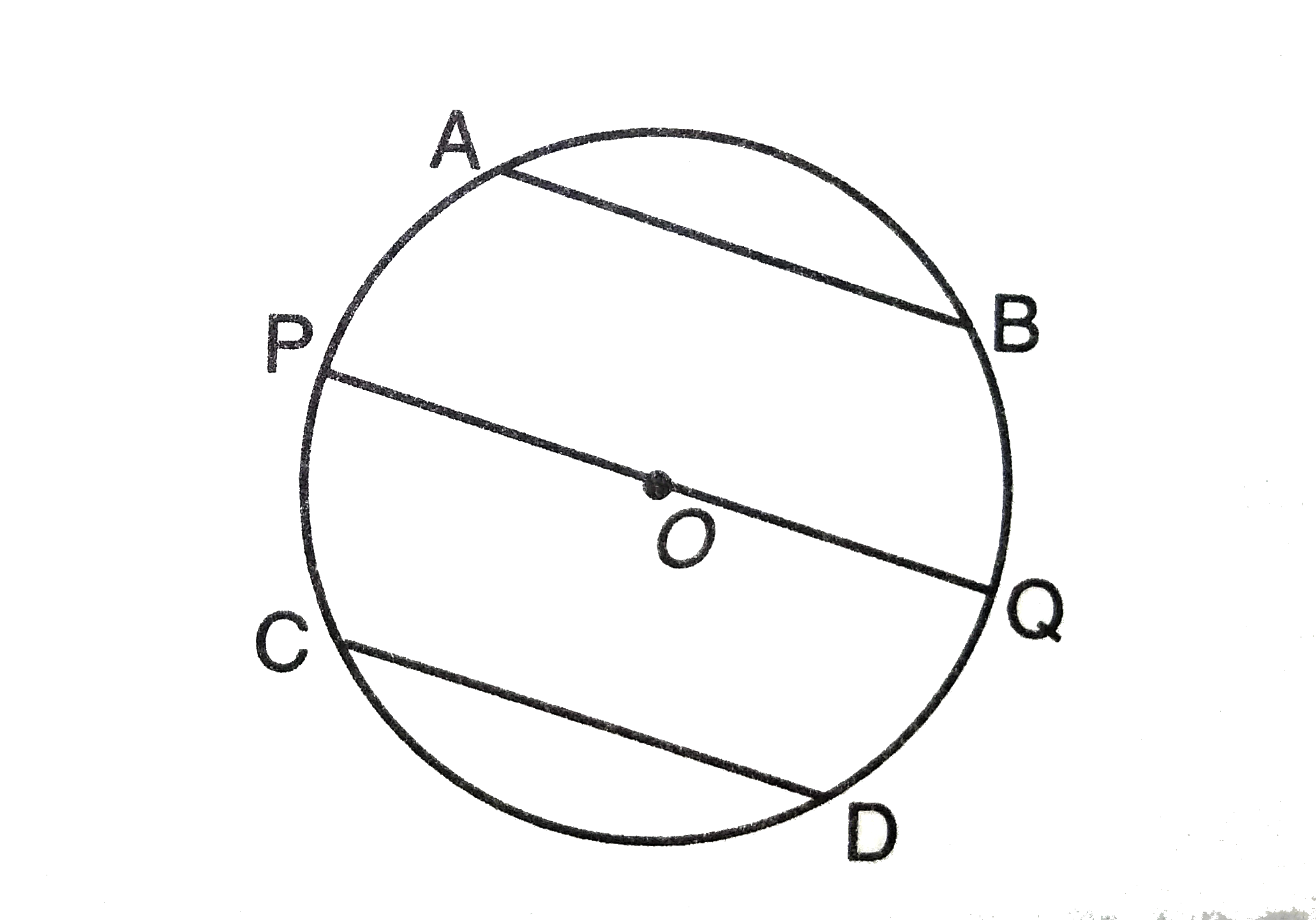
In the figure above, ¯¯¯¯¯¯PQ is a diameter of circle O, ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯PQ∣∣∣∣¯¯¯¯¯¯CD,and¯¯¯¯¯¯AB=¯¯¯¯¯¯CD. The length of chord ¯¯¯¯¯¯AB is 34 of the length of diameter ¯¯¯¯¯¯PQ. If r represents the radius length of circle O, what is the distance between chords ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD in terms r?
View Solution