The instantaneous velocity of a particle moving in xy-plane is →V=(ay)ˆi+(V0)ˆj where y is the instantaneous y co-ordinat of the particle and V0 is the particle starts from origin then its trajectory is


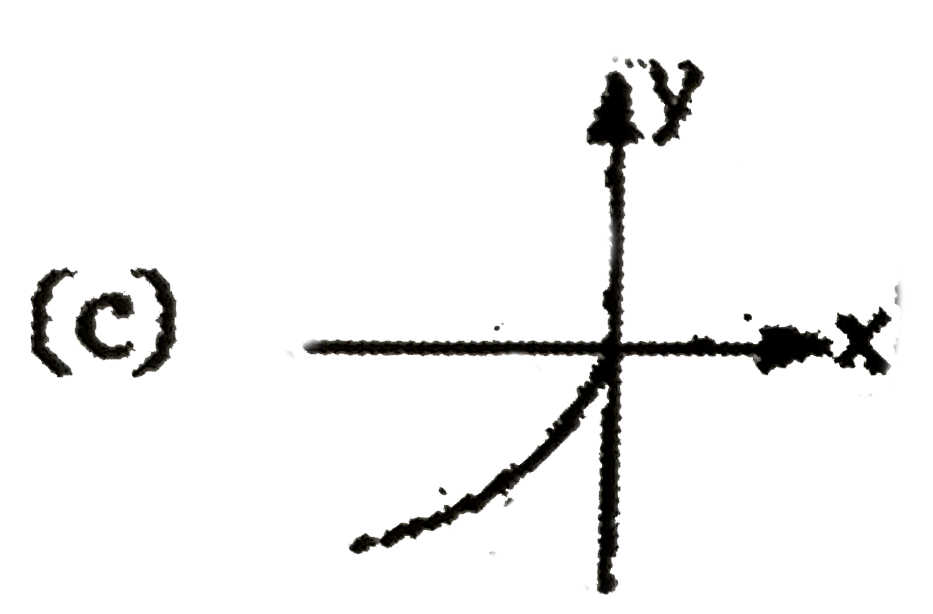
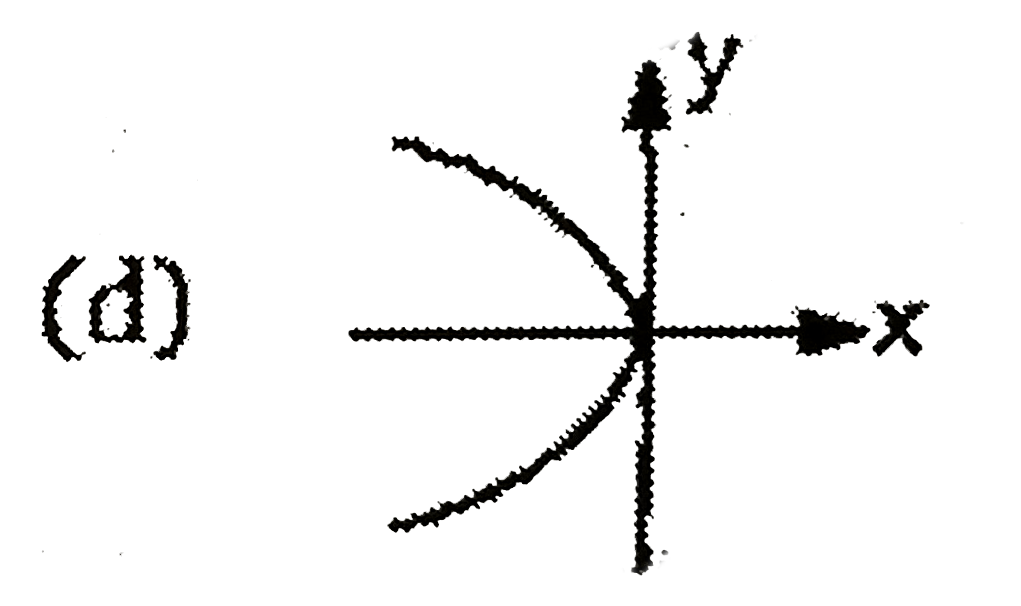
The correct Answer is:A
Step by step video, text & image solution for The instantaneous velocity of a particle moving in xy-plane is vecV=(ay)hati+(V_(0))hatj where y is the instantaneous y co-ordinat of the particle and V_(0) is the particle starts from origin then its trajectory is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-2
25 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Example
127 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
Similar Questions
The instantaneous velocity of a particle moving in a straight line is given as a function of time by: v=v0(1−(tt0)n) where t0 is a constant and n is a positive integer . The average velocity of the particle between t=0 and t=t0 is 3v04.Then , the value of n is
View SolutionThe figure shows a circular path taken by a particle. If the instantaneous velocity of the particle is →v=(2m/s)ˆi−(2m/s)ˆj, through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise around the circle? For both cases, draw →v on the figure.
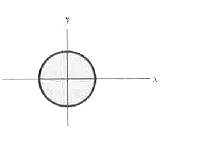
View Solution
Knowledge Check
Let v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
A|a|Bv.avCthe component of a parallel to vDthe component of a perpendicular to vPosition vectors of a particle moving in xy plane at time t is →r=a(1−cosomηt)ˆi+asinωtˆj. The path of the particle is
Aa circle of radius a and center at (a,0)Ba circle of radius a and center at (0,0)Can ellipseDneither a circle nor an ellipseVelocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
Ay=bx3/2a+cBy=4√2b3(xa)3/2+cCy=4√2b3(xa)3/2−cDy=bx3/2a−c
Instantaneous velocity of a particle moving in +x direction is given as v=3x2+2. At t=0, particle starts from origin. Find the average velocity of the particle between the two points p(x=2) and Q(x=4) of its motion path.
View SolutionA particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View SolutionA particle moves in plane with acceleration →a=2ˆi+2ˆj. If →v=3ˆi+6ˆj, then final velocity of particle at time t=2s is
View SolutionA particle moves in the x−y the accoding to the equatio, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution
