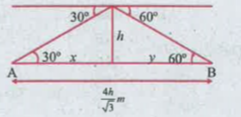
From the top of a lighhouse, the angles of depression of two ships on the opposite sides of it are observed to be 30∘and60∘. If the height of the lighthouse is h meters and thhe line joining the ships passes through the foot of the lighthouse. show that the distance between the ships is 4h√3 m.Solution in Tamil
Step by step video & image solution for From the top of a lighhouse, the angles of depression of two ships on the opposite sides of it are observed to be 30^(@) and 60^(@). If the height of the lighthouse is h meters and thhe line joining the ships passes through the foot of the lighthouse. show that the distance between the ships is (4h)/(sqrt(3)) m. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRYBOOK - SURA PUBLICATIONCHAPTER - TRIGONOMETRYEXERCISE - EXECRISE 5.4
9 Videos
- TRIGONOMETRYBOOK - SURA PUBLICATIONCHAPTER - TRIGONOMETRYEXERCISE - EXECRISE 5.5
15 Videos
- TRIGONOMETRYBOOK - SURA PUBLICATIONCHAPTER - TRIGONOMETRYEXERCISE - EXECRISE 5.2
9 Videos
- SURAS MODEL QUESTION PAPER-2019BOOK - SURA PUBLICATIONCHAPTER - SURAS MODEL QUESTION PAPER-2019EXERCISE - Part-IV
3 Videos
Similar Questions
From the top of tree of height 13m the angle of elevation and depression of the top and bottom of another tree are 45∘and30∘ respectively. Find the height of the seconds tree. (√3=1.732).
View SolutionThe value of sin2θ+11+tan2θ is equal to
View SolutionFind the angle of elevation of the top of a tower from a point on the ground, which is 30 m away the foot of a tower of height 10√3m.
View SolutionConstruct a △PQR in which the base PQ=4.5 cm, ∠R=45∘ and the median from R to RG is 6cm.
View Solutionएक प्रकाश स्तम्भ के शीर्ष से उसके विपरीत दिशाओं में दो जहाजों के अवनमन कोण α व β है|यदि प्रकाश स्तम्भ की ऊँचाई h मीटर है तथा जहाजों को मिलाने वाली रेखा प्रकाश स्तम्भ के तल से होकर जाती है| तो सिद्ध कीजिए की दोनों जहाजों के बीच की दुरी h(tanα+tanβ)tanαtanβ है|
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View Solutionएक प्रकाश-स्तम्भ के शीर्ष से, विपरीत दिशाओं में स्थित दो जहाजों के अवनमन कोण 30∘ और 45∘ हैं। यदि प्रकाश-स्तम्भ की ऊँचाई 90 मीटर है तथा दोनों जहाजों को मिलाने वाली रेखा प्रकाश-स्तम्भ के पाद से होकर जाती है, तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए।
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View SolutionTwo ships are sailing in the sea on the two side of lighthouse of height 10 m . The angle of elevation to the top of lighthouse observed from the ships are 30^@ and 45^@ then distance between two ship is [use sqrt(3)=1.7 ]
View Solutionஒரு கலங்கரை விளக்கத்தின் உச்சியிலிருந்து எதிரெதிர்பக்கங்களில் உள்ள இரண்டு கப்பல்கள் 30∘ மற்றும் 60∘இறக்கக் கோணத்தில் பார்க்கப்படுகின்றன.கலங்கரை விளக்கத்தின் உயரம் h மீ. இரு கப்பல்கள் மற்றும் கலங்கரை விளக்கத்தின் அடிப்பகுதி ஆகியவை ஒரே நேர்கோட்டில் அமைகின்றன எனில், இரண்டு கப்பல்களுக்கு இடைப்பட்ட தொலைவு 4h√3 மீ என நிரூபிக்க.
View Solution60 मीटर ऊँचे प्रकाश स्तम्भ की चोटी से एक जहाज का अवनमन कोण 60 है तो प्रकाश स्तम्भ पद से जहाज की दूरी ज्ञात कीजिए।
View SolutionThe angles of depression of two ships from the top of a lighthouse are 45∘and30∘. If the ships are 120 m apart, then find the height of the lighthouse.
View SolutionFrom the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and p. If the height of the lighthouse is h m etres and the line joining the ships passes through the foot of the lighthouse, show that the distance betw een the ships is
h(tanα+tanβ)tanαtanβ
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View SolutionFrom the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 30∘. If the height of the lighthouse is 100 m, then find how far is that ship from the lighthouse.
View Solution
