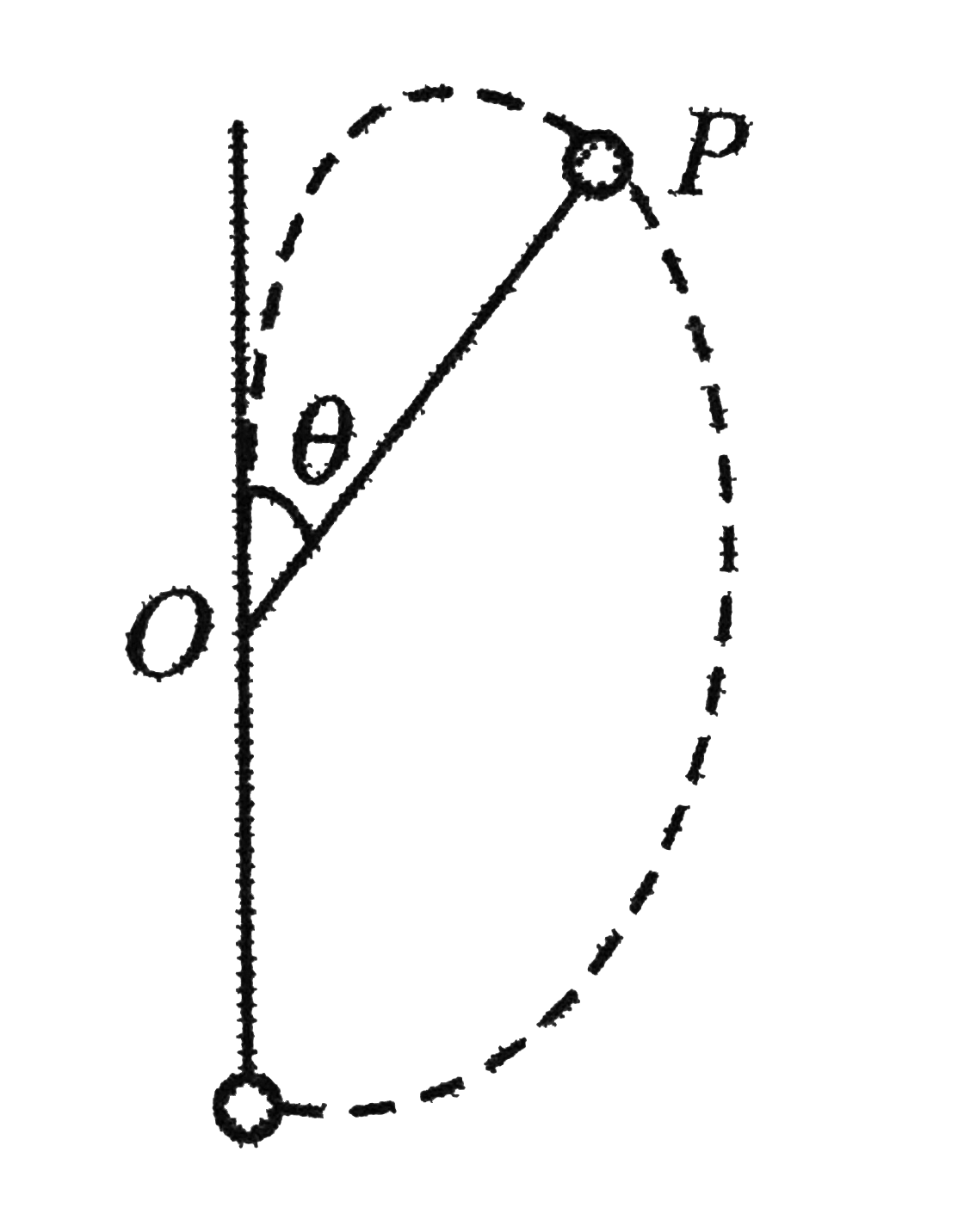
A block of mass m is tied with an inextensible light string of lengthl. One end of the string is fixed at point 0. Block is released (from rest) at A. Find acceleration of particle during its motion in vertical plane at positions specified in column-1 and match them with column-2. Given that A and O are at same horizontal level.

Column -1Column -2(A)Highest point(P)Acceleration is horizontal(B)At lowest point(Q)Acceleration is vertically(C)At θ=tan−1(√2)with vertical(R)Acceleration is vertically downwards(S)Acceleration has both horizontal and vertical components
The correct Answer is:A - R; B - Q; C - S
Step by step video, text & image solution for A block of mass m is tied with an inextensible light string of lengthl. One end of the string is fixed at point 0. Block is released (from rest) at A. Find acceleration of particle during its motion in vertical plane at positions specified in column-1 and match them with column-2. Given that A and O are at same horizontal level. {:(,"Column -1",,"Column -2",),((A),"Highest point",(P),"Acceleration is horizontal",),((B),"At lowest point",(Q),"Acceleration is vertically",),((C),"At " theta = tan^(-1) (sqrt2) "with vertical",(R),"Acceleration is vertically downwards",),(,,(S),"Acceleration has both horizontal and vertical components",):} by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The system shown in figure is released is released from rest . Find acceleration of different string blocks and tenson in different strings.

View SolutionThe pulley is light and smooth: the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.

View Solution
Knowledge Check
Two balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
A3:5B4:5C2:5D1:2
A point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.

View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View SolutionThe strings are inextensible and light: the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.

View SolutionTwo blocks are attached by a light inextensible string and the system is pulled by applying a force F0 as shown in the diagram. Find the acceleration of each block and tension in the string.

View Solution
