A pendulum is released from point A as shown in figure. At some instant net force on the bob is making and angle θ with the string. Then match the following:

Column-1 Column-2(A)Forθ=30∘(P) Particle may be moving between B & A(B)Forθ=120∘(Q) Particle may be moving between C & B particle is at A(C)Forθ=90∘(R) Particle is at A(D)Forθ=0∘(S) Particle is at B(T) None
The correct Answer is:A - Q,P; B - T; C - R; D - S
Step by step video, text & image solution for A pendulum is released from point A as shown in figure. At some instant net force on the bob is making and angle theta with the string. Then match the following: {:(,"Column-1",," Column-2"),("(A)",For theta=30^(@),,"(P) Particle may be moving between B & A"),("(B)",For theta = 120^(@),,"(Q) Particle may be moving between C & B particle is at A"),("(C)",For theta=90^(@),,"(R) Particle is at A"),("(D)",For theta=0^(@),,"(S) Particle is at B"),(,,,"(T) None"):} by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A pendulum is released from point A as shown in figure. At some instant net force one the bob is making an angle θ with the string. Then Match the following

Table-1Table-2(A)For θ=30∘(P)Particle may be moving along BA(B)For θ=120∘(Q)Particle may be moving along CB(C)For θ=90∘(R)Particle may be at A(D)For θ=0∘(S)Particle is at B(T)NoneView SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ) - Question 2 - Select One
A particle initially at rest is released from A as shown in figures. The approximate variation of direction of resultant acceleration as particle moves from A to B is :
 AclockwiseBanticlockwiseCdirection does not changesDnone of these
AclockwiseBanticlockwiseCdirection does not changesDnone of these - Question 3 - Select One
The angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
AA=2BBA=B2CA = BDAB = 1
Match the column:

∣∣ ∣ ∣ ∣ ∣ ∣∣Column -1Column -2(A)θ=37∘(P)f is upwards(B)θ=45∘(Q)f is downwards(C)θ=53∘(R)f is static(S)f is kinetic∣∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
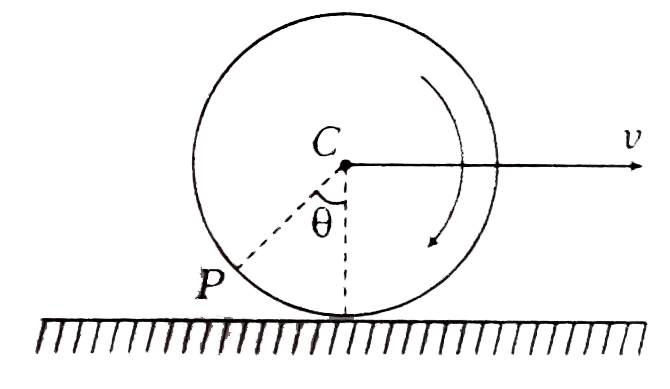
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3vView SolutionA vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2View SolutionSuppose that acosθ=b and csinθ=d, for θ and some constants a, b, c, d. Then which of the following is true?
View SolutionThe distance between the points (acosθ+bsinθ,0) and (0,asinθ−bcosθ).
View Solution

