A horizontal rod rotates about a vertical axis through one end. A ring, which can slide along the rod witgour friction, is initially close to the axis and then slides to the other end of the rod. In this process, which of the following quantities will be conserved?
{L = angular momentum, ET = total kinetic energy, ER = rotational kientic energy.]
L only
L and ET only
L and ER only
ET only
The correct Answer is:B
Step by step video, text & image solution for A horizontal rod rotates about a vertical axis through one end. A ring, which can slide along the rod witgour friction, is initially close to the axis and then slides to the other end of the rod. In this process, which of the following quantities will be conserved? {L = angular momentum, E_(T) = total kinetic energy, E_(R) = rotational kientic energy.] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
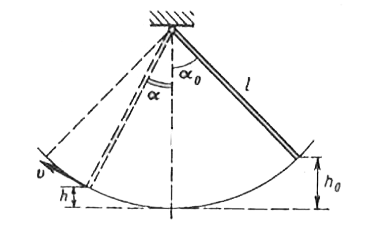
View SolutionA uniform. rod of length l can rotate without friction about an axis passing through its upper end (Fig). The rod is deflected by an angle a0 and let go. Find the speed of the lower end of the rod as a function of the angle α
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
 Athe normal reaction on the bead will be constant h magnitude and direction bothBthe magnitude of the normal reaction on the bead will be variableCthe magnitude of friction force on the bead will be constantDthe magnitude of friction force on the bead will be variable
Athe normal reaction on the bead will be constant h magnitude and direction bothBthe magnitude of the normal reaction on the bead will be variableCthe magnitude of friction force on the bead will be constantDthe magnitude of friction force on the bead will be variable - Question 2 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation - Question 3 - Select One
A horizontally orientied unifrom copper rod of length l is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is σ and density of copper is ρ.
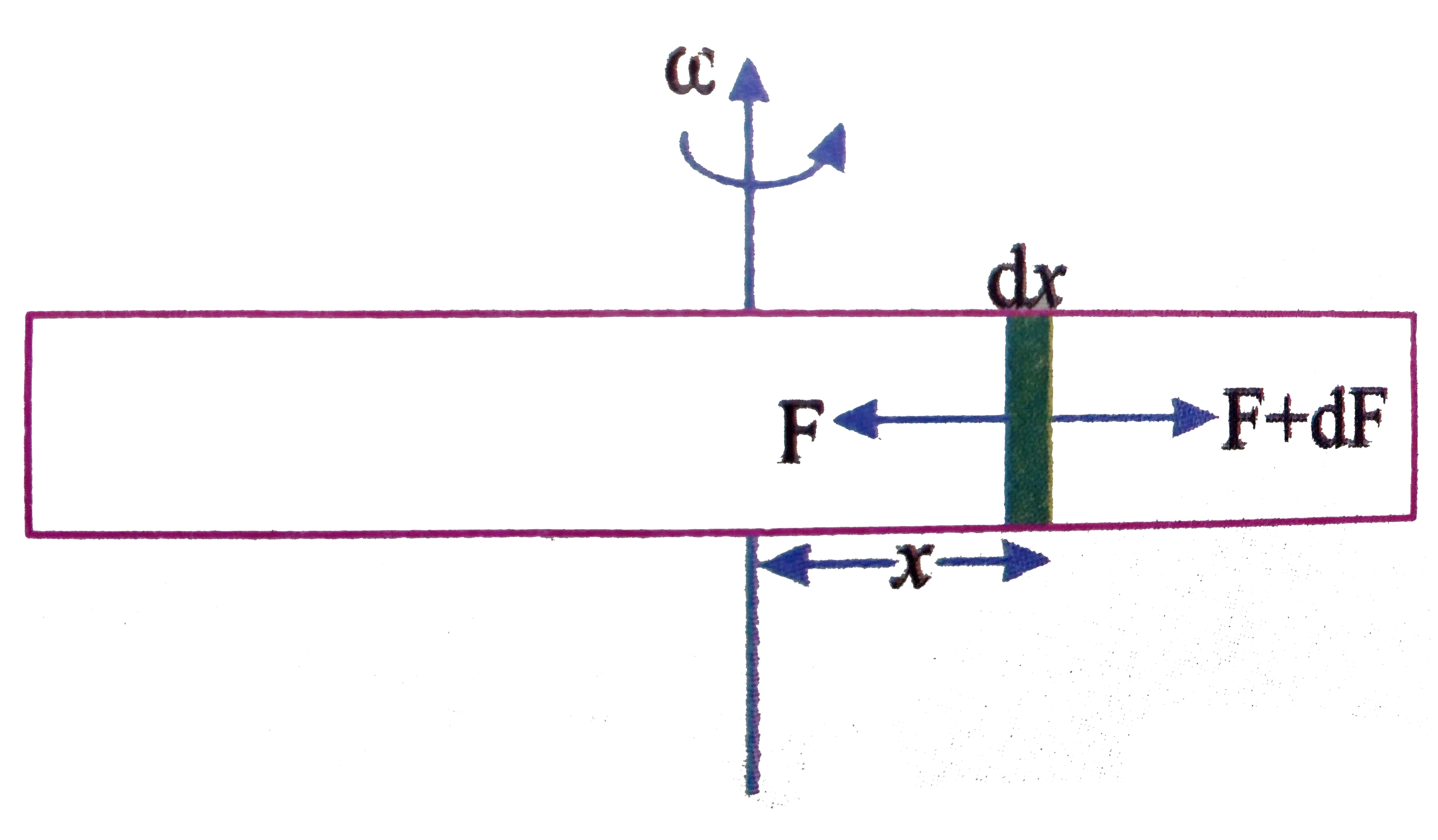 A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmp
A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmp
A uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
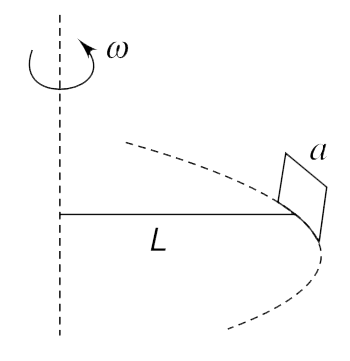
View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
 View Solution
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View SolutionA thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?
 View Solution
View SolutionA thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :
 View Solution
View Solution

