Two identical sound S1 and S2 reach at a point P is phase. The resultant loudness at point P is n dB higher than the loudness of S1 the value of n is :
2
3
4
6
The correct Answer is:D
Step by step video, text & image solution for Two identical sound S_1 and S_2 reach at a point P is phase. The resultant loudness at point P is n dB higher than the loudness of S_1 the value of n is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The resultant loudness at a point P is n dB higher than the loudness of S1 whoch is one of the two identical sound sources S1 and S2 reaching at that point in phase. Find the value of n.
View SolutionTwo identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.View Solution
Knowledge Check
- Question 1 - Select One
Two identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
A2B4C5D6 - Question 2 - Select One or More
Sounds from two identical sources S1 and S2 reach a point P. When the sounds reach directly, and in the same phase, the intensity at P is I0. The power of S1 is now reduced by 64% and the phase difference between S1 and S2 is varied continuously. The maximum and minimum intensities recorded at P are now Imax and Imin
AImax=0.64I0BImin=0.36I0CImax/Imin=16DImax/Imin=1.64/0.36 - Question 3 - Select One
Two sources of sound S1andS2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0 . (a) If theta equals 45∘, what will be the intensity of sound detected at this point if one of the sources is switched off ? (b) What will be the answer of the previous part if θ=60∘ ?
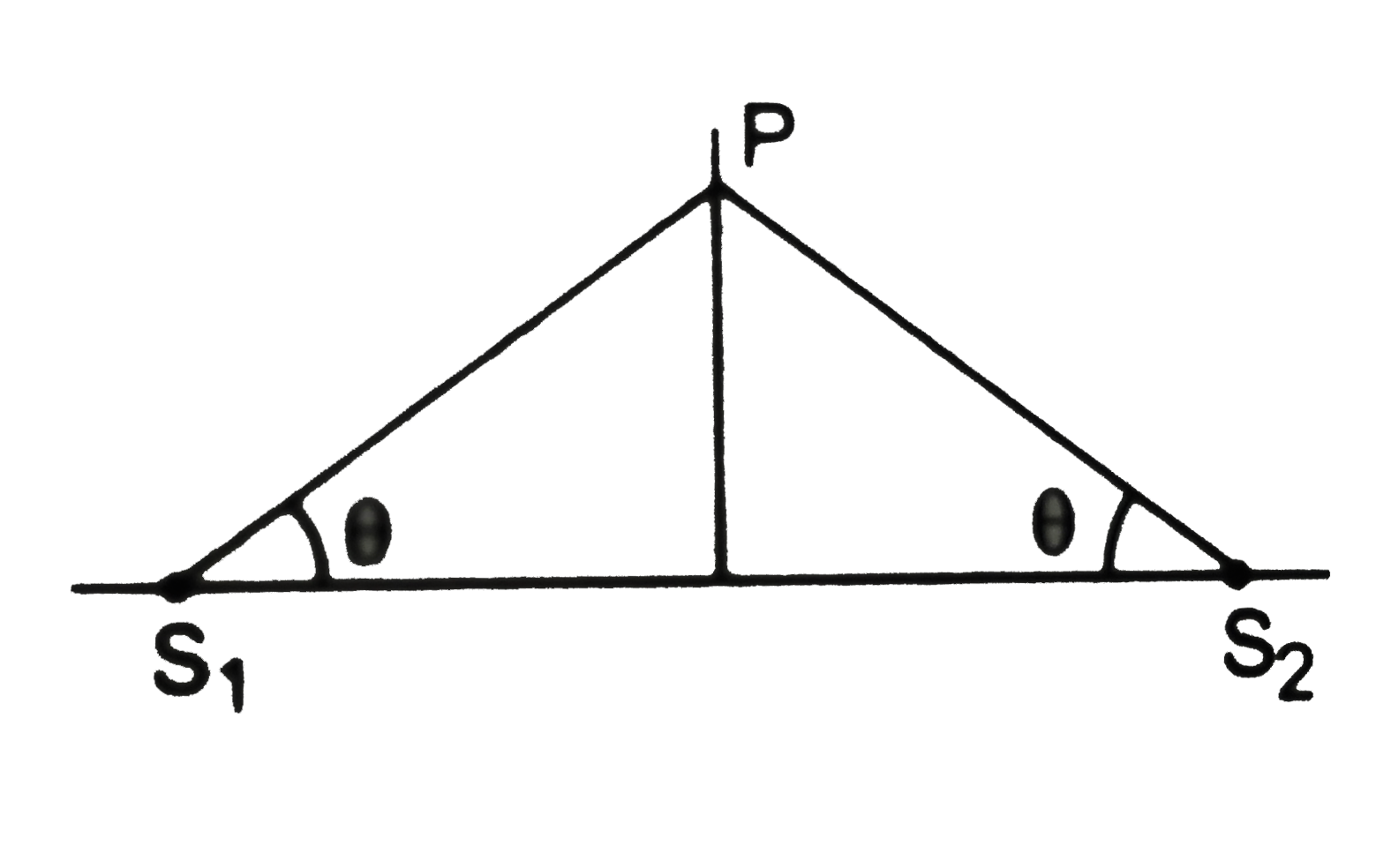 AI04,I02BI02,3I04CI04,I04DI02,I04
AI04,I02BI02,3I04CI04,I04DI02,I04
In Fig. , two point sources S1 and S2 which are in phase and separated by distance D=1.5λ , emit identical sound waves of wavelength λ.
(a) What is the path length difference of the waves from S1 and S2 at point P1, which lies on the perpendicular bisector of distance D, at a distance greater than D from the sources ? (That is, what is the difference in the distance from source S1 to point P1 and the distance from source S2 to P1?) What type of interference occurs at P1 ?
(b) What are the path length difference and type of interference at point P2 in fig.
(c ) Figure shows a circle with a radius much greater than D, centered on the midpoint between sources S1 and S2. What is the number of points N around this circle at which the interference is fully constructive? (That is, at how many points do the waves arrive exactly in phase?)View SolutionConsider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
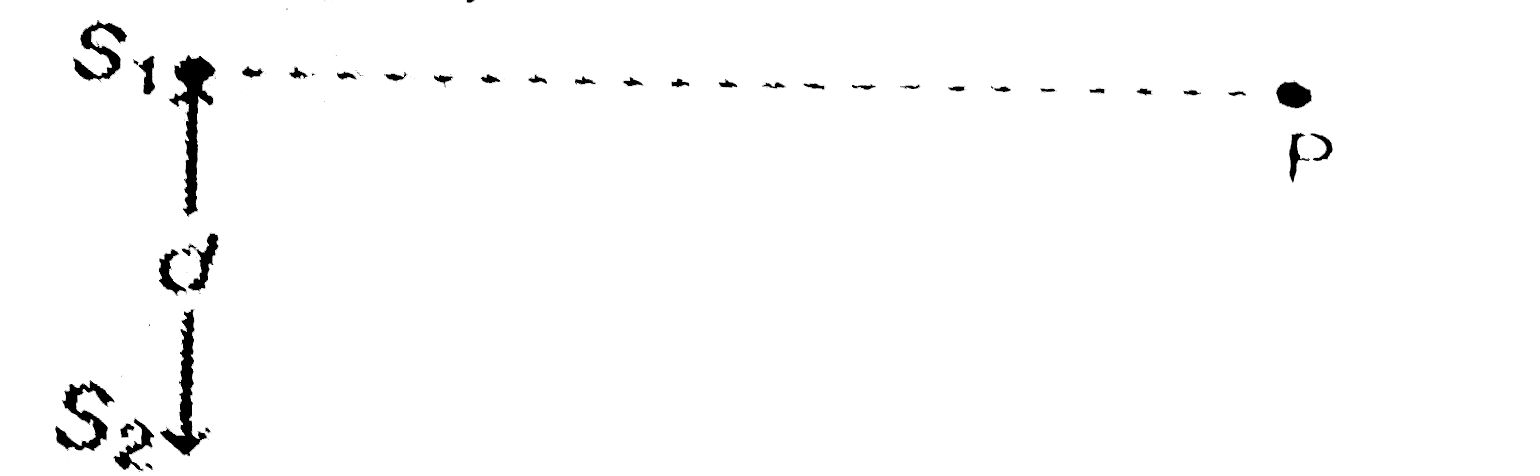 View Solution
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionTwo sound waves each of wavelength λ and having the same amplitude A form two sources S1andS2 interfere at a point P. If the path difference S2P−S1P=λ3, then the amplitude of the resultant were at P will be
View SolutionWhen beats are produced by two progressive waves of same amplitude and of nearly same frequencies then the maximum loudness of the resulting sound is n times the loudness of each of the component wave trains. The value of n is
View Solution

