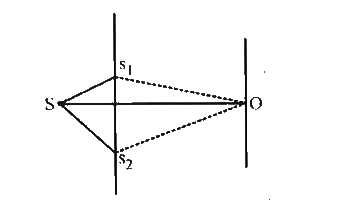
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Distance d between S1andS2 is
![In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S(1) and S(2) are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S(1) and S(2). P is a point on the screen 1 mm from O at which path difference between waves from S(1) and S(2) is 11250Å. Position of amy point on the screen can be expressed by theta. The path difference is zero at O and a central bright fringe of intensity I(0) is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is (1)/(90) radian. Answer the following question [assume D to be large and theta very small so taht sinapproxtantheta approxtheta] Q. Distance d between S(1) and S(2) is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DPP_PHY_2_3_E01_130_Q01.png)
0.2 mm
45μm
20μm
none of these
The correct Answer is:B
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - QUESTION BANK
37 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Matching Column Type
2 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
In Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View Solution
Knowledge Check
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Fringe width when screen is at position (1) will be
 A49mmB35mmC45mmD14mm
A49mmB35mmC45mmD14mmIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Intensity at point Q when screen is at position (1) is
 A0.5 I0B5I0CzeroDnone of these
A0.5 I0B5I0CzeroDnone of theseIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Intensity at P when the screen is at positio (1), is
 A2I0BI0CI02DI04
A2I0BI0CI02DI04
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (1), phase difference of waves from S1 and S2 at point P is effectively.

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Angular position of a bright fringe of order 5 when the screen is at position (1), will be nearly

View SolutionIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (2), its distance from the double slits is nearly

View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
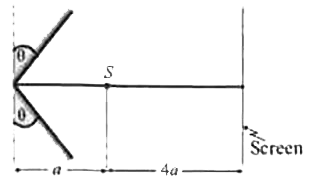
View SolutionThere are two plane mirrors. They are mutually inclined as shown in figure. S is a source of monochromatic light of wavelength λ. The reflected beam interfere and fringe pattern is obtained on the screen. If θ is small, the fringe width will be :
View Solution
