Question

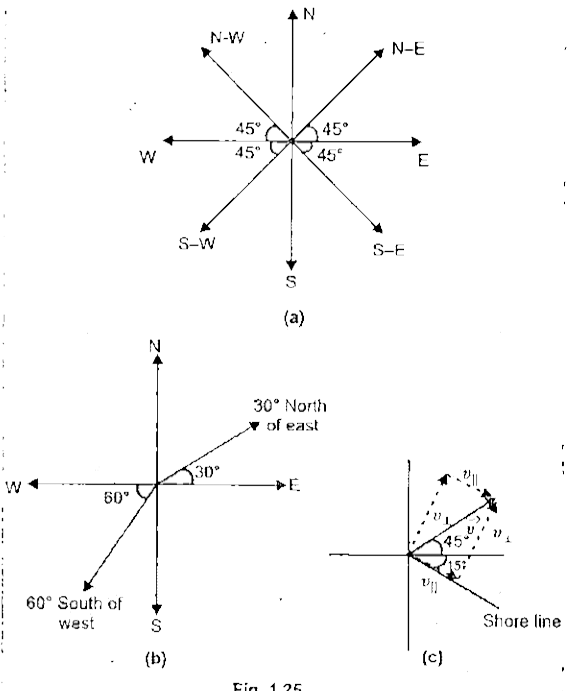
A man rows a boat with a speed of 18 km/hr in northwest direction. The shoeline makes an angle of ${15}^{\circ }$ south of west. Obtain the component of the velocity of the boat along the shoreline:

Options

A. 9 km/hr
B. `18 sqrt(3)/2` km/hr
C. `18 cos 15^(@)` km/hr
D. `18 cos 75^(@)` km/hr

Answer

A

Explanation

To solve the problem, we need to find the component of the boat's velocity along the shoreline. Here are the steps to solve the problem:

Step 1: Understand the Directions
The boat is moving in the northwest direction, which is at an angle of 45 degrees from the positive x-axis (east) towards the negative y-axis (south). The shoreline makes an angle of 15 degrees south of west, which is equivalent to 15 degrees from the negative x-axis (west) towards the negative y-axis (south).

Step 2: Define the Angles
- The direction of the boat (northwest) can be represented as:
- Angle from the positive x-axis (east) = 180° - 45° = 135°.

- The direction of the shoreline (15 degrees south of west) can be represented as:
- Angle from the positive x-axis (east) = 180° + 15° = 195°.

Step 3: Calculate the Components of the Boat's Velocity
The speed of the boat is given as 18 km/hr. We can break this speed into its x (east-west) and y (north-south) components using trigonometric functions.

- x-component (Vx):
\( V_x = V \cdot \cos(\theta) = 18 \cdot \cos(135°) \)

- y-component (Vy):
\( V_y = V \cdot \sin(\theta) = 18 \cdot \sin(135°) \)

Step 4: Calculate the Values
Using the values of cosine and sine for 135 degrees:
- \(\cos(135°) = -\frac{1}{\sqrt{2}}\)
- \(\sin(135°) = \frac{1}{\sqrt{2}}\)

Now substituting these values:
- x-component:
\( V_x = 18 \cdot \left(-\frac{1}{\sqrt{2}}\right) = -\frac{18}{\sqrt{2}} \approx -12.73 \text{ km/hr} \)

- y-component:
\( V_y = 18 \cdot \left(\frac{1}{\sqrt{2}}\right) = \frac{18}{\sqrt{2}} \approx 12.73 \text{ km/hr} \)

Step 5: Find the Component of Velocity Along the Shoreline
To find the component of the boat's velocity along the shoreline, we need to project the velocity vector of the boat onto the direction of the shoreline.

The angle between the boat's direction (135°) and the shoreline direction (195°) is:
\( \Delta \theta = 195° - 135° = 60° \)

Using the formula for the projection of one vector onto another:
\( V_{shoreline} = V \cdot \cos(\Delta \theta) \)
Where \(V\) is the magnitude of the boat's velocity (18 km/hr).

Substituting the values:
\( V_{shoreline} = 18 \cdot \cos(60°) = 18 \cdot \frac{1}{2} = 9 \text{ km/hr} \)

Final Answer
The component of the velocity of the boat along the shoreline is 9 km/hr.

---