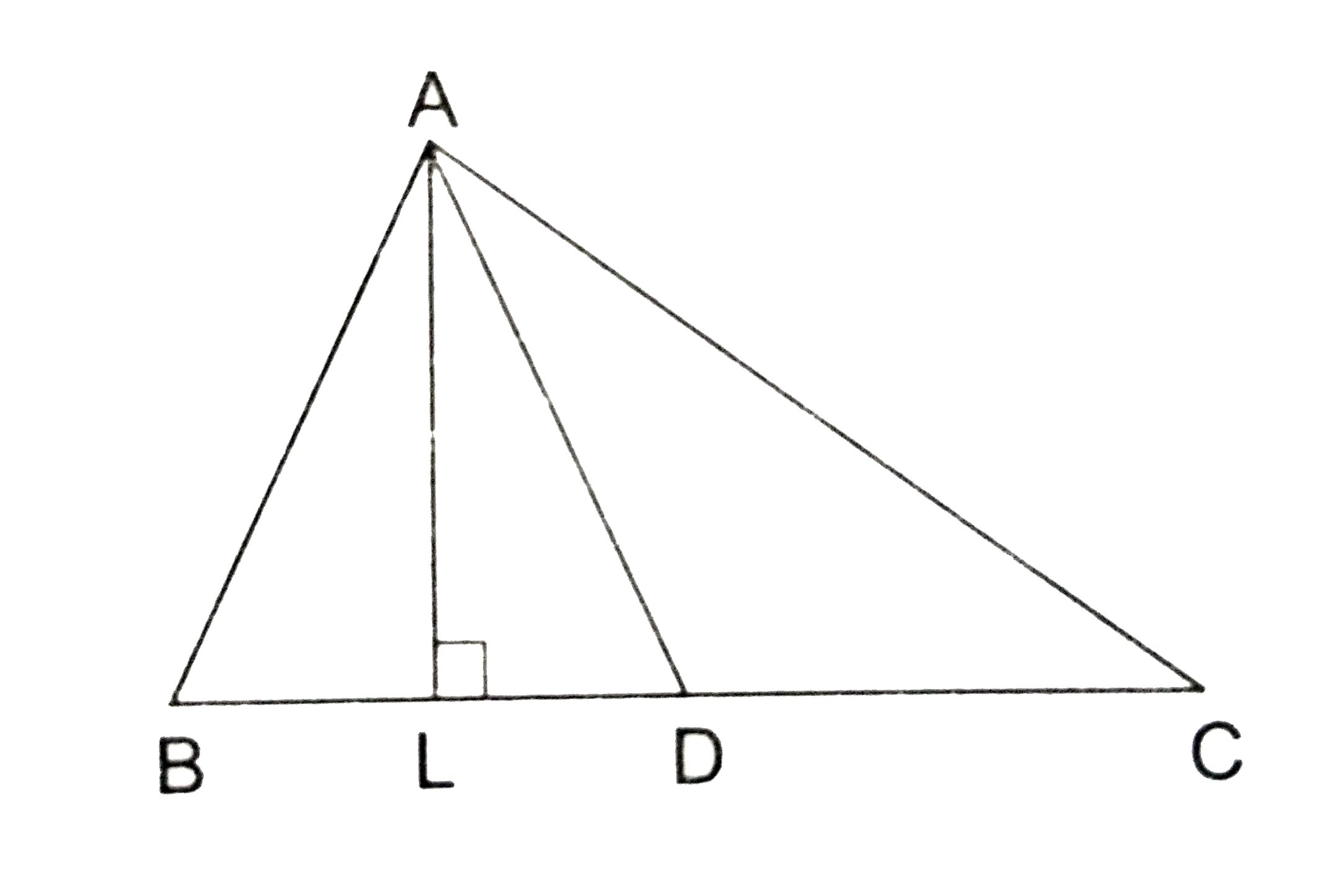
Seg AD is the median of triangleABC and AM|BC. Prove that : (i) AC^2=A

Seg AD is the median of $△ A B C$ and $A M ⊥ B C$ . Prove that : $(i) A C^{2} = A D^{2} + B C \times D M + {(\frac{B C}{2})}^{2}$ $(i i) A B^{2} = A D^{2} - B C \times D M + {(\frac{B C}{2})}^{2}$ .

View Solution

AD is a median of triangle ABC. Prove that : $A B + B C + A C > 2 A D$

View Solution

In $a Δ A B C, A D$ is a median and $A L ⊥ B C$ .
Prove that
(a) $A C^{2} = A D^{2} + B C \cdot D L + {(\frac{B C}{2})}^{2}$
(b) $A B^{2} = A D^{2} - B C \cdot D L + {(\frac{B C}{2})}^{2}$
(c) $A C^{2} + A B^{2} = 2 A D^{2} = 2 A D^{2} + \frac{1}{2} B C^{2}$
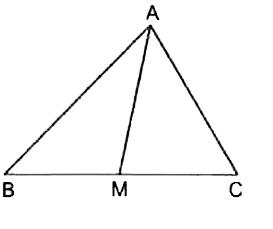
ocr_image

View Solution

AM is median of $△ A B C$ , prove that (AB+BC+CA) $> 2 A M$ .
ocr_image

View Solution

In a triangle $A B C, A C > A B$ , $D$ is the mid-point of $B C$ and $A E ⊥ B C$ . Prove that: (i) $A B^{2} = A D^{2} - B C D E + \frac{1}{4} B C^{2}$ (ii) $A B^{2} + A C^{2} = 2 A D^{2} + \frac{1}{2} B C^{2}$

View Solution

In acute angled triangle ABC, AD is median and AE is altitude , prove that:
(i) $A C^{2} = A D^{2} + B C \times D E + \frac{1}{4} B C^{2}$
(ii) $A B^{2} = A D^{2} - B C \times D E + \frac{1}{4} B C^{2}$
(iii) $A C^{2} + A B^{2} = 2 A D^{2} + \frac{1}{2} B C^{2}$

View Solution

In equilateral $△ A B C, A D ⊥ B C .$ Prove that $3 B C^{2} = 4 A D^{2} .$

View Solution

In a triangle $A B C, A C > A B$ , $D$ is the mid-point of $B C$ and $A E ⊥ B C$ . Prove that: (i) $A B^{2} = A D^{2} - B C x D E + \frac{1}{4} B C^{2}$

View Solution

In Figure 2, $A D ⊥ B C$ . Prove that $A B^{2} + C D^{2} = B D^{2} + A C^{2}$ .

View Solution

In a $Δ A B C, ∠ B$ is an acute-angle and $A D ⊥ B C$
Prove that :
(i) $A C^{2} = A B^{2} + B C^{2} - 2 B C \times B D$
(ii) $A B^{2} + C D^{2} = A C^{2} + B D^{2}$

View Solution

Seg AD is the median of $△ A B C$ and $A M ⊥ B C$ . Prove that : $(i) A C^{2} = A D^{2} + B C \times D M + {(\frac{B C}{2})}^{2}$ $(i i) A B^{2} = A D^{2} - B C \times D M + {(\frac{B C}{2})}^{2}$ .

Similar Questions

Recommended Questions

Seg AD is the median of △ABC and AM⊥BC. Prove that : (i)AC2=AD2+BC×DM+(BC2)2 (ii)AB2=AD2−BC×DM+(BC2)2.

1)In∠AMC AC2=AM2+MC2−(1) In∠AMD AD2=AM2+MD2 AM2=AD2−DM2−(2) AC2=AD2−DM2+MC2 AC2=AD2+(BC2)2+2⋅DM⋅BC2 AC2=AD2+DM⋅BC+(BC2)2 In∠ABM AB2=BM2+AM2 AB2=BM2+AD2−DM2 AB2=AD2+(BD−MD)2−DM2 AB2=AD2+BD2+MD2−2⋅BD⋅MD−DM2 AB2=AD2+(BC2)2−2⋅BC22⋅DM AB2=AD2−BC⋅DM÷(BC2)2.

Similar Questions

Recommended Questions

Seg AD is the median of $△ A B C$ and $A M ⊥ B C$ . Prove that : $(i) A C^{2} = A D^{2} + B C \times D M + {(\frac{B C}{2})}^{2}$ $(i i) A B^{2} = A D^{2} - B C \times D M + {(\frac{B C}{2})}^{2}$ .