Refer to the collision of two blocks on a frictionless table. Before the collision, the block of mass m iss at rest.

Q. What is the total momentum of the blocks just AFTER THE COLLISION?
If the collision were elastic, what is the total kinetic energy of the block just AFTER the collision?
16J
32J
64J
128J
The correct Answer is:D
In an elastic collision, momentum and kinetic energy are conserved. If we calculate the initial kinetic energy, we can see that only the moving 4 kg block has kinetic energy K=12mv2=12(4)(8)2=128J
Topper's Solved these Questions
Similar Questions
A block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View Solution
Knowledge Check
In , if the collision were perfectly elastic, what would be the speed of deuteron after the collision ?
A2×106ms−1B4×106ms−1C6×106ms−1D8×106ms−1In an inelastic collision, the kinetic energy after collision
Ais same as before collisionBis always less than before collisionCis always greater than before collisionDmay be less or greater than before collisionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 AkL22MB√MkL(c)SCML2kDzero
AkL22MB√MkL(c)SCML2kDzero
A body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionA steel ball weighting 1 kg is fastened to a cord 1 m long and is released when the cord is horizontal . At the bottom of its path the ball strikes a 5-kg steel block initially at rest on a frictionless surface . The collision is elastic . Find the speed of the ball and speed of the block just after collision . (g = 9.8ms−2)
[Hint : Apply principal of conservation of momentum and conservation of kinetic energy as the collision is elastic .]
View SolutionIn the figure shown the block A collides head on with another block B at rest. Mass of B is twice the mass of A. The block A stops after collision. The co-efficient of restitution is :
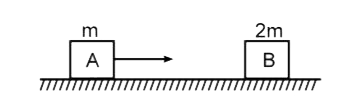
View SolutionThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
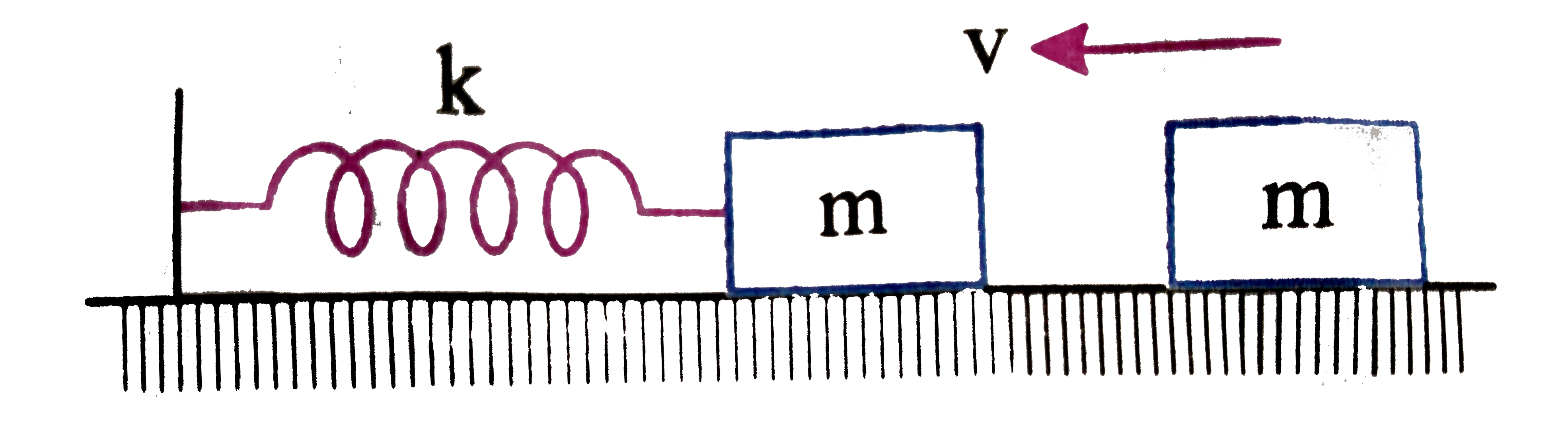
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View Solution
