A battery of emf 5V and internal resistance 20Ω is connected to a combination of two resistance 50Ω and 40Ω in series. If the p.d. across the 50Ω resistor is measured by a voltmeter of resistance 1000Ω, what will be the percentage error?
The correct Answer is:2.7%
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the total resistance in the circuit
The total resistance (R_total) in the circuit is the sum of the internal resistance of the battery (r_battery) and the resistances of the two resistors in series (R1 and R2).
Given:
- rbattery=20Ω
- R1=50Ω
- R2=40Ω
Rtotal=rbattery+R1+R2=20+50+40=110Ω
Step 2: Calculate the current in the circuit
Using Ohm's law, we can calculate the current (I) flowing through the circuit using the formula:
I=VRtotal
Where:
- V=5V (emf of the battery)
I=5110≈0.04545A
Step 3: Calculate the potential difference across the 50Ω resistor
The potential difference (V_R1) across the 50Ω resistor can be calculated using:
VR1=I×R1
Substituting the values:
VR1=0.04545×50≈2.2725V
Step 4: Calculate the resistance of the voltmeter in parallel with the 50Ω resistor
The resistance of the voltmeter (R_voltmeter) is given as 1000Ω. When connected in parallel with the 50Ω resistor, the equivalent resistance (R_eq) can be calculated using the formula:
Req=R1×RvoltmeterR1+Rvoltmeter
Substituting the values:
Req=50×100050+1000=500001050≈47.619Ω
Step 5: Calculate the new current in the circuit with the voltmeter
The new total resistance in the circuit (R_total_new) will now include the equivalent resistance of the voltmeter:
Rtotal_new=rbattery+Req+R2=20+47.619+40=107.619Ω
Now, calculate the new current (I_new):
Inew=VRtotal_new=5107.619≈0.0465A
Step 6: Calculate the potential difference measured by the voltmeter
The potential difference (V_measured) across the equivalent resistance is:
Vmeasured=Inew×Req
Substituting the values:
Vmeasured=0.0465×47.619≈2.22V
Step 7: Calculate the percentage error
The percentage error can be calculated using the formula:
Percentage Error=(Vtrue−VmeasuredVtrue)×100
Where Vtrue is the true value (2.2725 V) and Vmeasured is the measured value (2.22 V):
Percentage Error=(2.2725−2.222.2725)×100≈2.30%
Final Answer
The percentage error in the measurement is approximately 2.30%.
---
The total resistance (R_total) in the circuit is the sum of the internal resistance of the battery (r_battery) and the resistances of the two resistors in series (R1 and R2).
- rbattery=20Ω
- R1=50Ω
- R2=40Ω
Using Ohm's law, we can calculate the current (I) flowing through the circuit using the formula:
- V=5V (emf of the battery)
The potential difference (V_R1) across the 50Ω resistor can be calculated using:
The resistance of the voltmeter (R_voltmeter) is given as 1000Ω. When connected in parallel with the 50Ω resistor, the equivalent resistance (R_eq) can be calculated using the formula:
The new total resistance in the circuit (R_total_new) will now include the equivalent resistance of the voltmeter:
The potential difference (V_measured) across the equivalent resistance is:
The percentage error can be calculated using the formula:
The percentage error in the measurement is approximately 2.30%.
Topper's Solved these Questions
- GALVANOMETERS: AMMETER AND VOLTMETERSBOOK - NN GHOSHCHAPTER - GALVANOMETERS: AMMETER AND VOLTMETERSEXERCISE - Exercise
32 Videos
- FUNDAMENTAL OF CURRENT ELECTRICITYBOOK - NN GHOSHCHAPTER - FUNDAMENTAL OF CURRENT ELECTRICITYEXERCISE - Exercises
45 Videos
- GAUSS THEOREM AND ITS APPLICATIONBOOK - NN GHOSHCHAPTER - GAUSS THEOREM AND ITS APPLICATIONEXERCISE - EXAMPLES(a)
24 Videos
Similar Questions
A battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View SolutionA cell of emf 2V and internal resistance 4Ω is connected across a parallel combination of two resistors of resistance 10Ω and 20Ω. Find the current through each resistor using Kirchhoff's laws.
View Solution
Knowledge Check
A battery having e.m.f. 5 V and internal resistance 0.5Ω is connected with a resistance of 4.5Ω then the voltage at the terminals of battery is
A4.5 VB4 VC0 VD2 VA battery having e.m.f. 5 V and internal resistance 0.5Ω is connected with a resistance of 4.5Ω then the voltage at the terminals of battery is
A4.5VB4VC0VD2VA voltmeter of resistance 200Ω is used to measure p.d across resistances 100Ω and 200Ω.
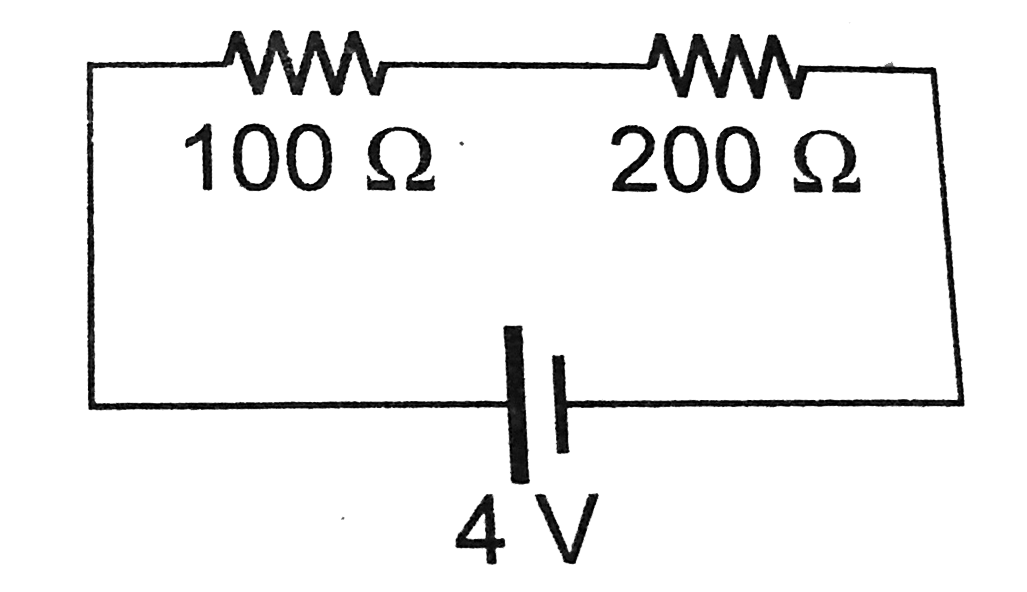 .AThe voltmeter reads 1V, when connected across 100ΩBThe voltmeter reads 2V, when connected across 200ΩCBoth (1) and (2)DNone
.AThe voltmeter reads 1V, when connected across 100ΩBThe voltmeter reads 2V, when connected across 200ΩCBoth (1) and (2)DNone
A battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
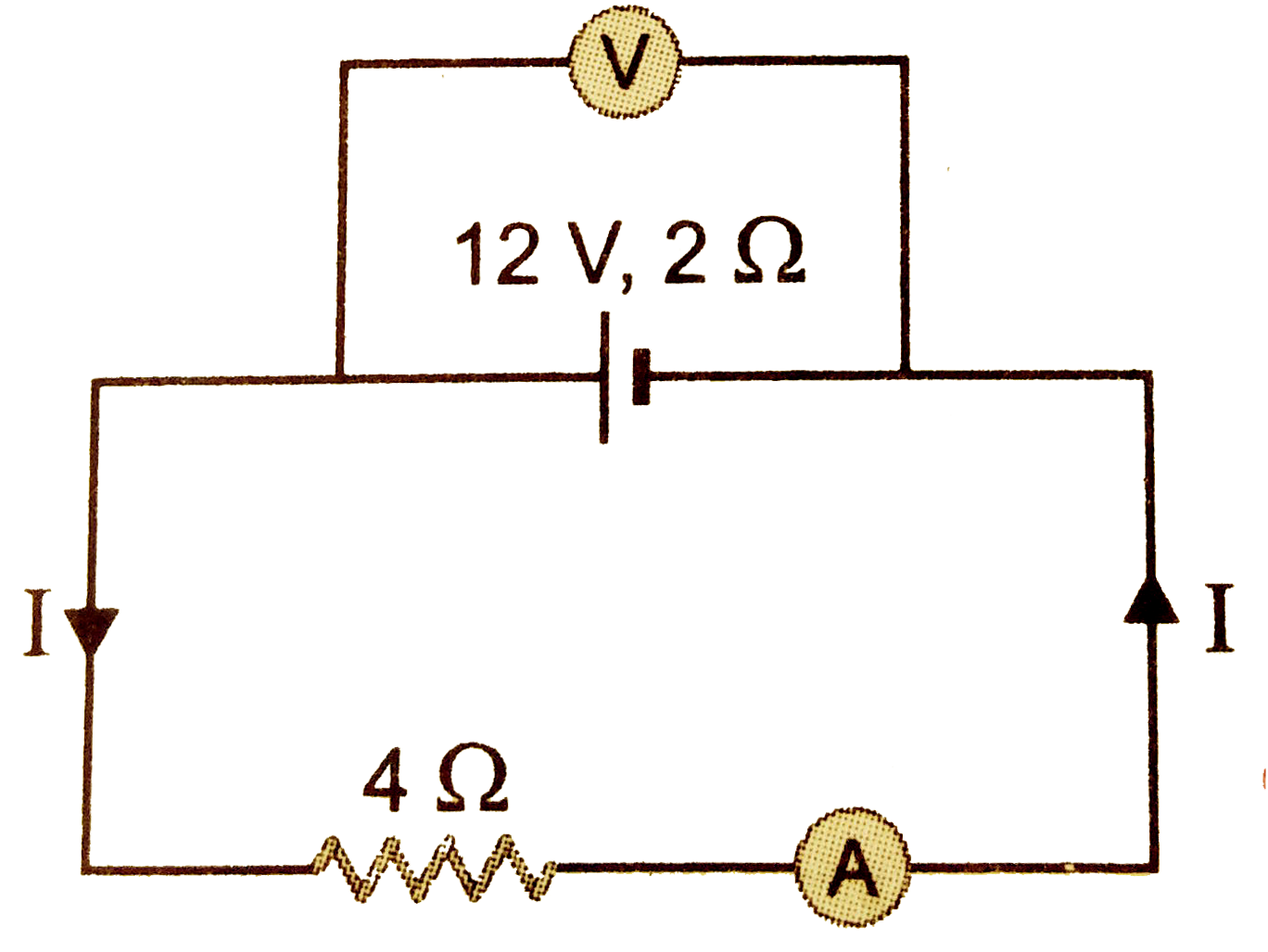
View SolutionA battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the Fig. Show that a voltmeter when placed across the cell and across the resistor, in turn, gives the same reading.
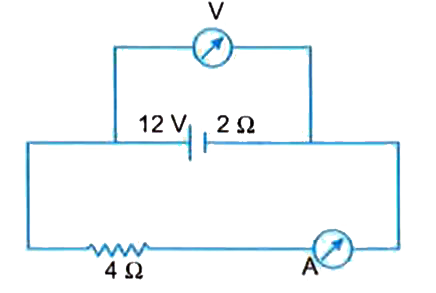
View SolutionThe series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
View SolutionThe series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View SolutionThe battery of EMF 5V and internal resistance 20Ωis connected with a resistance R1=50Ω and a resistance . A voltmeter of resistance 1000Ω is used to measure the potential difference across R1 .What percentage error is made in the reading.
View Solution
