Calculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
The correct Answer is:λ4πε0In√l2+a2+1√l2+a2−1
Step by step video, text & image solution for Calculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =lambda) of length 2l at a distance a from the centre of the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE21videos
ELECTRIC FIELD AND POTENIAL
- BOOK - NN GHOSHCHAPTER - DYNAMO, MOTOR, TRANSFORMEREXERCISE - EXERCISE8videos
DYNAMO, MOTOR, TRANSFORMER
- BOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B18videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Find the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionFind : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.View Solution
Knowledge Check
- Question 1 - Select One
Find the electric field at point P (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is a =√32L.
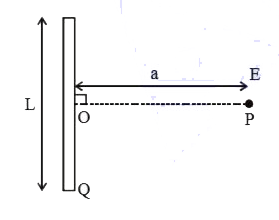 A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2 - Question 2 - Select One
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell - Question 3 - Select One
Find centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
A3l4(3a+b2a+b)B3l4(2a+b3a+b)Cl4(2a+b3a+b)Dl(2a+b3a+b)
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View SolutionIf the linear density of a rod of length L varies as λ=A+Bx , find the position of its centre of mass .
View SolutionThe electric field at a point P which is at a distance l on the perpendicular bisector of a uniformly charged wire of length 1 , charge Q=Q2πɛ0l2√k where k = ?
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionTwo mutually perpendicular long straight conductors carrying uniformly distributed charges of linear charges densities λ1 and λ2 are positon at a distance a from each other. How does the interaction between the rods depends on a ?
 View Solution
View Solution

