Question

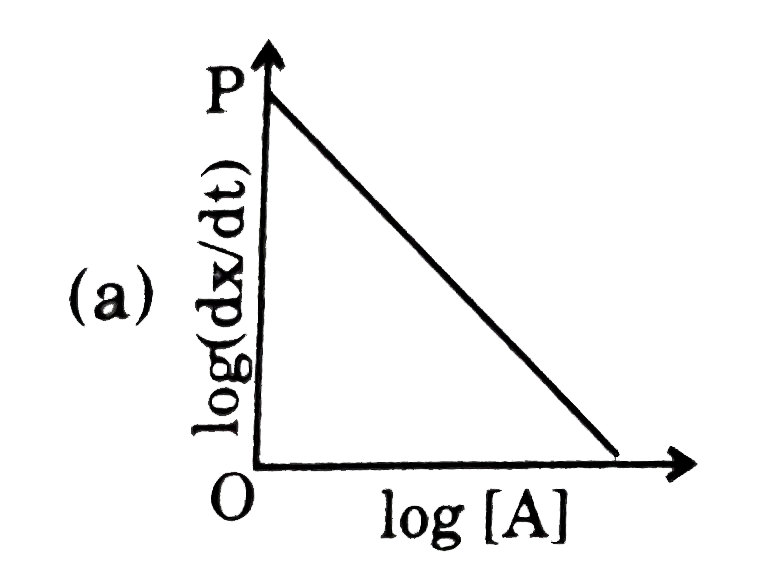
$A\to$ Product and $\left(\frac{dx}{dt}\right)=k{\left[A\right]}^2$. If log $\left(\frac{dx}{dt}\right)$ is plotted against log [A], then graph is of the type:

Options

A.
B.
C.
D.

Answer

C

Explanation

To solve the given problem step by step, we need to analyze the relationship between the rate of reaction and the concentration of reactant A.

1. Understand the Rate Law:
The rate of reaction is given by the equation:
\( \frac{dx}{dt} = k (A)^2 \)
where \( \frac{dx}{dt} \) is the rate of reaction, \( k \) is the rate constant, and \( (A) \) is the concentration of reactant A.

2. Take Logarithms:
To analyze the relationship graphically, we take the logarithm of both sides of the equation:
\( \log\left(\frac{dx}{dt}\right) = \log(k (A)^2) \)

3. Apply Logarithmic Properties:
Using the properties of logarithms, we can expand the right-hand side:
\( \log\left(\frac{dx}{dt}\right) = \log(k) + \log((A)^2) \)
\( \log\left(\frac{dx}{dt}\right) = \log(k) + 2\log((A)) \)

4. Rearranging the Equation:
We can rearrange this equation into the form of a straight line \( y = mx + c \):
\( \log\left(\frac{dx}{dt}\right) = 2\log((A)) + \log(k) \)
Here, we identify:
- \( y = \log\left(\frac{dx}{dt}\right) \)
- \( x = \log((A)) \)
- The slope \( m = 2 \)
- The y-intercept \( c = \log(k) \)

5. Graph Interpretation:
Since the slope \( m = 2 \) is positive, this indicates that as the concentration of A increases, the rate of reaction also increases. The graph of \( \log\left(\frac{dx}{dt}\right) \) versus \( \log((A)) \) will be a straight line with a positive slope.

6. Conclusion:
The correct type of graph when plotting \( \log\left(\frac{dx}{dt}\right) \) against \( \log((A)) \) is a straight line with a positive slope.

Final Answer:
The graph is of the type: Option C (a straight line with a positive slope).