What should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10m/s2)

12 kg
8 kg
10 kg
6 kg
The correct Answer is:D
Step by step video, text & image solution for What should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10 m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Conceptual MCQs
23 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
What should be minimum value of F so that 2 kg slides on ground but 1kg does not slide on it? [g=10msec2]
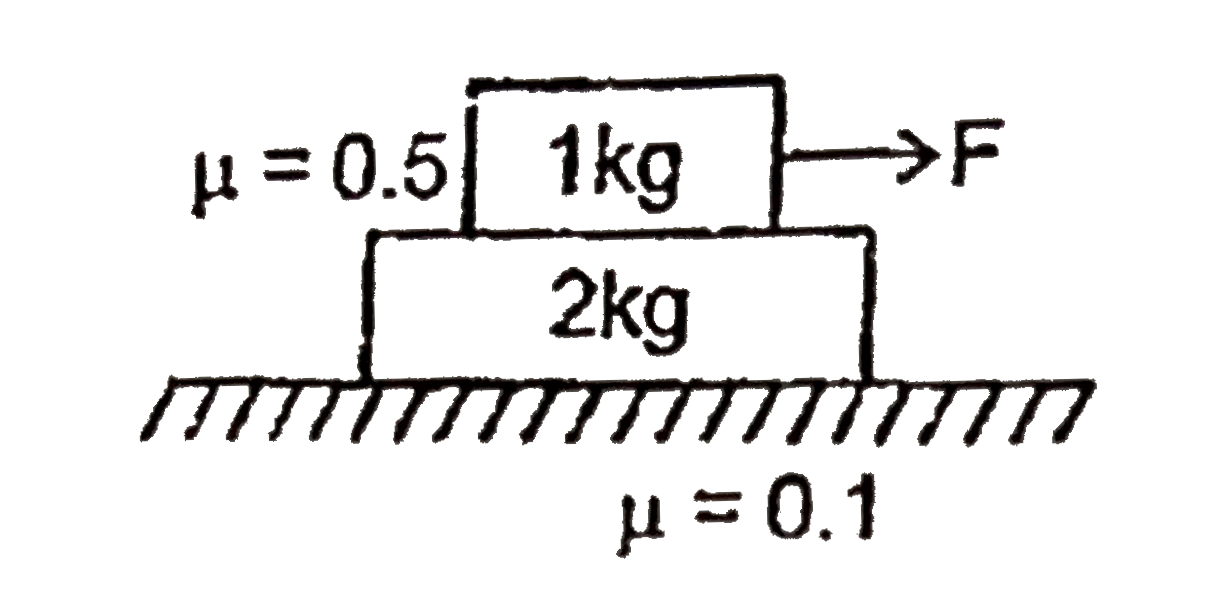
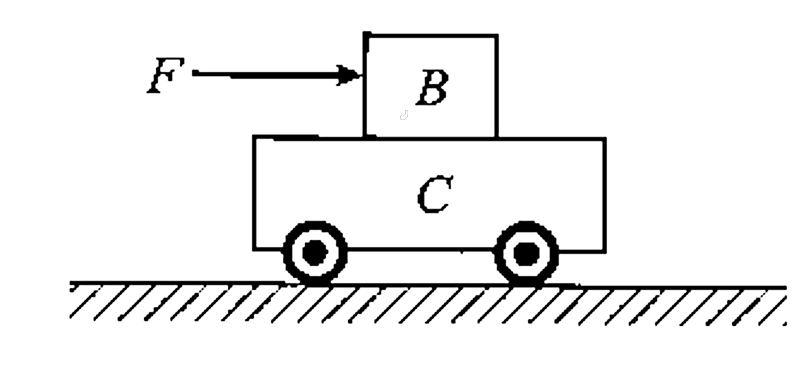
View SolutionMass of block B shown in figure-2.218 is m and that of cart C is M. Show that the maximum value of force F such that the block does not slip over the surface of C, has a magnitude
View Solution
Knowledge Check
The coefficient of static friction between the block of 2 kg and the table shown in figure is μs=02. What should be the maximum value of m so that the blocks does not move? Take g=10m/s2. The string and the pulley are light and smooth.
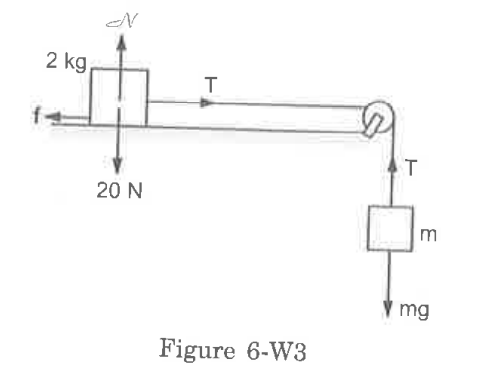 A0.4 kgB0.2 kgC0.1 kgD0.5 kg
A0.4 kgB0.2 kgC0.1 kgD0.5 kgIn the arrangement shown in figure mA=mB=2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient between blocks A and B is μ=0.5. What maximum horizontal force F can be applied so that block A does not slip over the block B? (g=10m/s2)
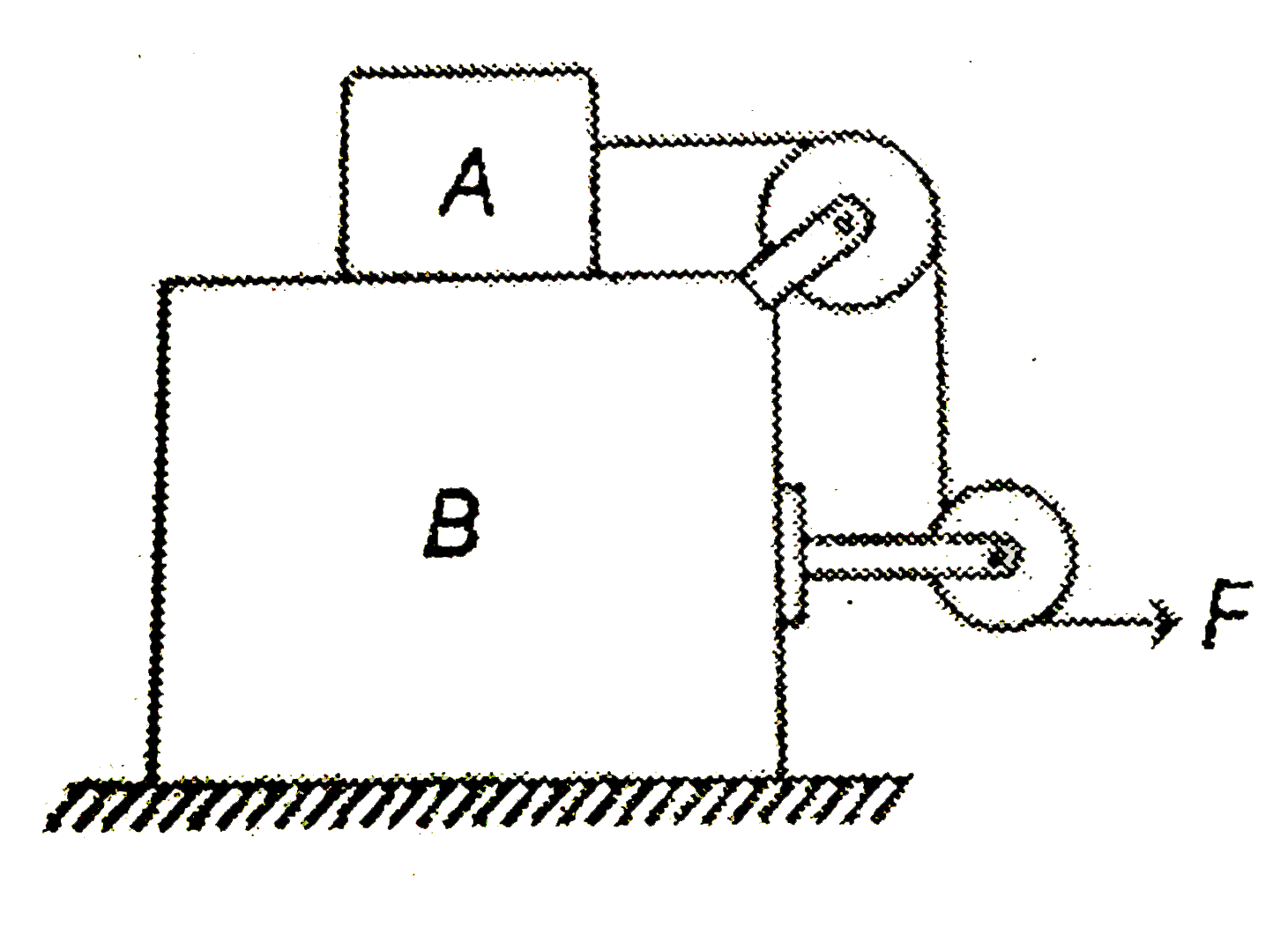 A25 NB40 NC30 ND20 N
A25 NB40 NC30 ND20 NA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
A4cmB5cmC10 cmD16 cm
Two blocks A and B of masses mA=1kgandmB=3kg are kept on the table as shown in figure. The coefficient of friction between A and B is 0.2 and between B and the surface of the table is also 0.2. The maximum force F that can be applied on B horizontally, so that the block A does not slide over the block B is ________ (in N): [Take g=10m/s2]

View SolutionA block of mass 0.5 kg rests on a wedge of mass 2 kg as in Fig. 7.87 . The wedge is acted on by a horizontal force F and slides on a frictionless surface . If the coefficient of static friction between the wedge and the block is μs=0.8 , and the angle of inclination is 30∘ , find the maximum and minimum values of F for which the block does not slip . Take (g = 10m/s2)

View SolutionThe coefficient of static friction, μs between block A mass 2kg and the table as shown in the figure, is 0.2. What would be the maximum mass value of block B, so that the two blocks do not move ? The string and the pulley are asseumed to be smooth and massless (g=10m/s2)

View SolutionThe coefficient of static friction, μs between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.(g=10m/s2)

View SolutionA system of two blocks is shown in figure. Friction coefficient between 5 kg and 10 kg block is μ=0.6 and between 10 kg and ground is μ=0.4 What will be the maximum value of force F applied at the lower block so that 5 kg block does not slip w.r.t. 10 kg . (g=10m/sec2). The force applied at the upper block is having fixed magnitude of 80 N (both forces start to act simultaneously)
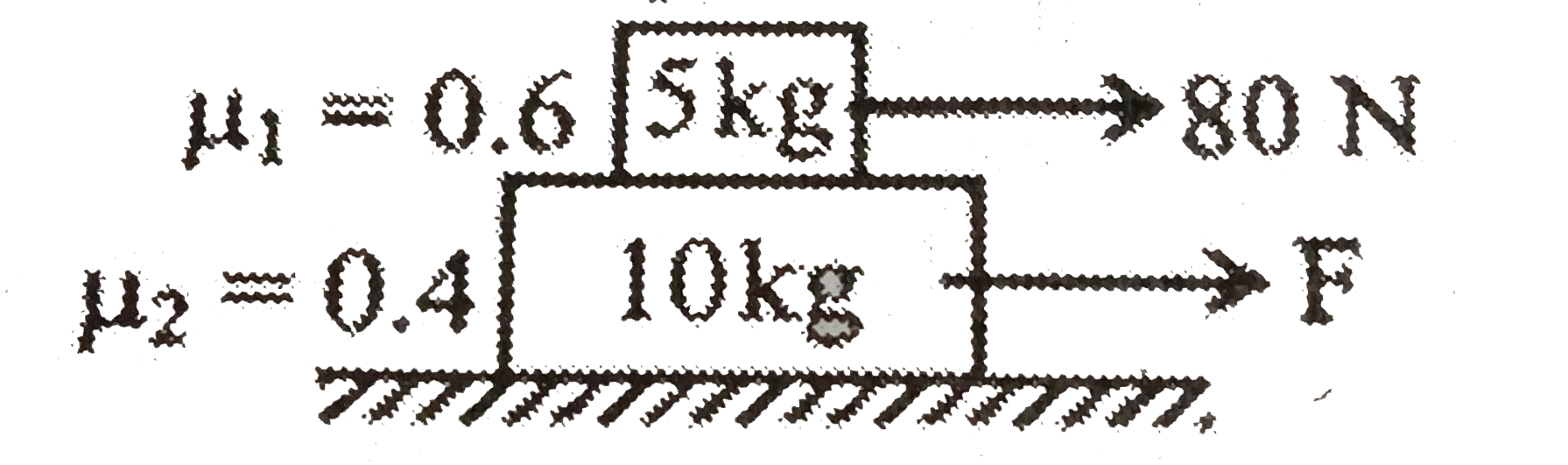
View Solution
