Two types of tickets were sold for a concert held at an amphitheater. Tickets to sit on a bench during the concert cost $75 each, and tickets to sit on the lawn during the concert cost $40 each. Organizers of the concert announced that 350 tickets had been sold and that $19,250 had been raised through ticket sales alone. Which of the following systems of equations could be used to find the number of tickets for bench seats, B, and the number of tickets for lawn seats, L, that were sold for the concert?
(75B)(40L)=1,950
B+L=350
40B + 75L = 19,250
B+L=350
75B + 40L =350
B+L=19,250
75B+40L=19,250
B+L=350
The correct Answer is:D
To solve the problem, we need to set up a system of equations based on the information provided about the ticket sales for the concert.
Step 1: Define the Variables
Let:
- B = number of bench tickets sold
- L = number of lawn tickets sold
Step 2: Set Up the First Equation
According to the problem, the total number of tickets sold is 350. This can be expressed as:
B+L=350
This equation represents the total number of tickets sold.
Step 3: Set Up the Second Equation
Next, we need to account for the total revenue generated from ticket sales. The revenue from bench tickets is 75B (since each bench ticket costs $75) and the revenue from lawn tickets is 40L (since each lawn ticket costs $40). The total revenue is given as $19,250. This can be expressed as:
75B+40L=19250
This equation represents the total revenue generated from ticket sales.
Step 4: Write the System of Equations
Now we have a system of two equations:
1. B+L=350
2. 75B+40L=19250
Conclusion
The system of equations that can be used to find the number of tickets for bench seats B and the number of tickets for lawn seats L sold for the concert is:
B+L=35075B+40L=19250
Let:
- B = number of bench tickets sold
- L = number of lawn tickets sold
According to the problem, the total number of tickets sold is 350. This can be expressed as:
B+L=350
This equation represents the total number of tickets sold.
Next, we need to account for the total revenue generated from ticket sales. The revenue from bench tickets is 75B (since each bench ticket costs $75) and the revenue from lawn tickets is 40L (since each lawn ticket costs $40). The total revenue is given as $19,250. This can be expressed as:
75B+40L=19250
This equation represents the total revenue generated from ticket sales.
Now we have a system of two equations:
1. B+L=350
2. 75B+40L=19250
The system of equations that can be used to find the number of tickets for bench seats B and the number of tickets for lawn seats L sold for the concert is:
B+L=35075B+40L=19250
Similar Questions
प्रातः 6:00 से प्रातः 10:00 बजे तक मापक किसी शहर में रेलवे टिकट खिड़की से विभिन्न शहरों के लिए बेचे गए टिकटों की संख्या संबंधी सूचना निम्न दंड-आलेख द्वारा दी गई है। इस दंड-आलेख को पढ़कर दिए गए प्रश्नों के उत्तर दीजिए।
(a) कुल कितने टिकट बेचे गए?
(d) किस शहर के लिए सबसे अधिक टिकट बेचे गए?
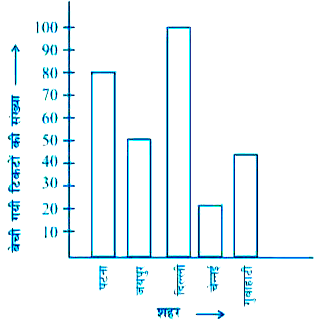
(c) किस शहर के लिए सबसे कम टिकट बेचे गए?
(d) उन शहरों के नाम बताओ जिनके लिए बेचे गए टिकटों की संख्या 20 से अधिक थी।
(e) रिक्त स्थानों की पूर्ति कीजिए -
दिल्ली और जयपुर के लिए बेचे गए कुल टिकटों की संख्या, पटना और चेन्नई के लिए कुल मिलाकर बेचे गए टिकटों की संख्या से अधिक थी।
View SolutionFor a journey the cost of a child ticket is 1/3 rd of the cost of an adult ticket. If the cost of the tickets for 4 adults and 5 children is Rs. 85, the cost of a child ticket is :
View SolutionSome tickets of ₹ 200 and some of ₹ 100, of a drama were sold at a theatre. The number of tickets of ₹ 200 sold was 20 more than the number of tickets of ₹ 100. The total amount received by the theatre, by sale of tickets, was ₹ 37,000. Find the number of ₹ 100 tickets sold.
View Solutionएका नाट्यगृहावर नाटकाची ₹ 200 दराची व ₹100 दराची काही तिकिटे विकली गेली. ₹ 200 दराच्या तिकिटांची संख्या 100 रुपयांच्या तिकिटांच्या संख्येपेक्षा 20 तिकिटे जास्त खपली होती. दोन्ही प्रकारच्या तिकिट विक्रीतून नाट्यगृहाला ₹ 37,000 मिळाले, तर 100 रुपयांची किती तिकिटे विकली गेली?
View Solutionएका नाट्यगृहावर नाटकाची ₹ 200 दराची व ₹100 दराची काही तिकिटे विकली गेली. ₹ 200 दराच्या तिकिटांची संख्या 100 रुपयांच्या तिकिटांच्या संख्येपेक्षा 20 तिकिटे जास्त खपली होती. दोन्ही प्रकारच्या तिकिट विक्रीतून नाट्यगृहाला ₹ 37,000 मिळाले, तर 100 रुपयांची किती तिकिटे विकली गेली?
View SolutionIn a circket match there are three types of tickets say A,B and C each costing Rs. 1,000 ,Rs. 500 and Rs. 200 respectively .The ratio of three ticket sold of category A,B and C is 3:2:5 . If the total collection from selling the tickets is Rs. 2.5 crore .find the total number of tickets sold ?
View SolutionIn a musical concert, 15% of the total is reserve for first class. If all the tickets were sold except 171 ticket of first class, then how many tickets were sold?
View SolutionIn a cricket match there are three types of tickets say A B and C each costing Rs. 1000, Rs. 500 and Rs. 200 respectively. The ratio of the tickets sold of categories A B and C is 3:2:5. If the total collection from selling the tickets Is Rs 2.5 crore, find the total number of tickets sold?
View Solution
