Four rods AB, BC, CD and DA have mass m,2m,3m and 4m respectively. The center of mass of all the four rods
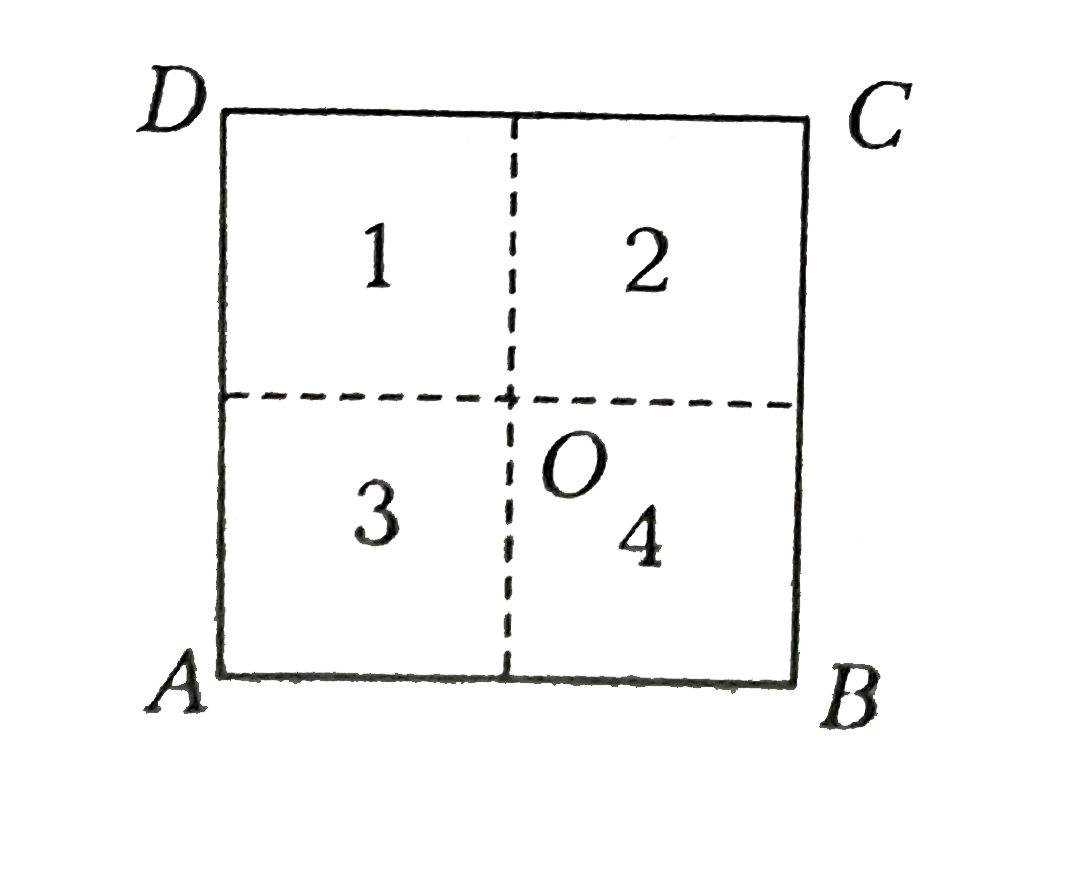
lie in region 1
lie in region 2
lie in region 3
lie at 0
The correct Answer is:A
C1→ Position of center of mass of rods AB and CD(nearer to CD, as it is heavy)

C2→ Position of center of mass of rods BC and DA.
Crightarrrow Overall center of masss of all four rods and it lies in region 1.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason21videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
Four particles A,B,CandD of masses m,2m,3mand4m respectively are placed at corners of a square of side x as shown in Fig.

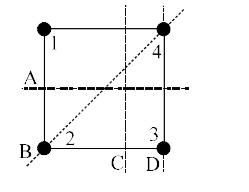
Locate the centre of mass.View SolutionIn the adjacent diagram, objects 1 and 2 each have mass m while objects 3 and 4 each have mass 2m. Note four lines A, B, C and D. The center of mass of the system is most likely to be at the intersection of lines :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure four rods AB,BC,CD and DA have mass m, 2m, 3m and 4m respectively In Which of the regions (numberd 1,2,3,4) the centre of mass of system lies?
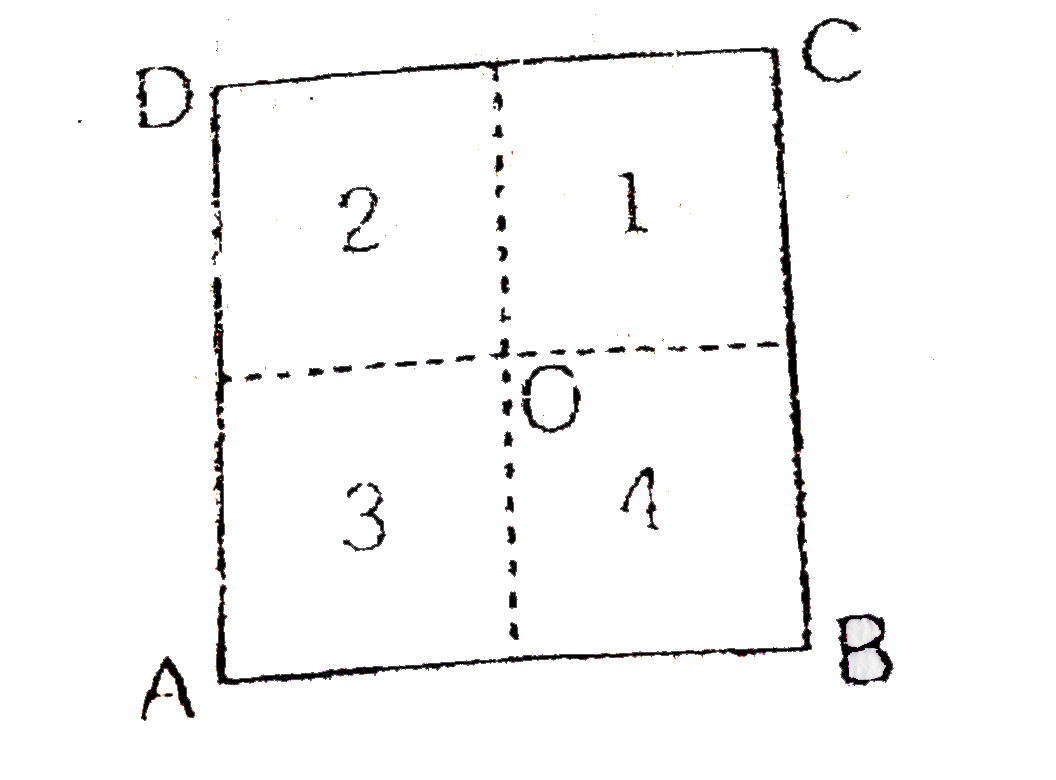 A1B2C3D4
A1B2C3D4 - Question 2 - Select One
Four rods of equal lengths AB,BC,CD and DA have mass m,2m,3m and 4m respectively are place in x-y plane (see figure) given AB=BC=CD=DA=4 meters. The centre of mass of the system will satisfy (x and y are in meters)
 Ax>2,y>2Bx>2,y<2Cx>2,y<2Dx>2,y>2
Ax>2,y>2Bx>2,y<2Cx>2,y<2Dx>2,y>2 - Question 3 - Select One
Four particles A, B, C and D with masses mA=m,mB=2m,mC=3mandmD=4m are at the corners of a square. They have accelerations of equal magnitude with directions as shown. The acceleration of the centre of mass of the particles is:
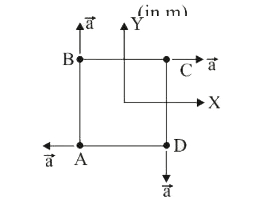 Aa5(ˆi−ˆj)Ba(ˆi+ˆj)Ca5(ˆi+ˆj)Dzero
Aa5(ˆi−ˆj)Ba(ˆi+ˆj)Ca5(ˆi+ˆj)Dzero
Four particles having masses, m, wm, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View Solutionfour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionOne end of a thin uniform rod of length L and mass M1 is rivetted to the center of a uniform circular disc of radius r and mass M2 so that both are coplanar. The center of mass of the combination from the center of the disc is (Assume that the point of attachment is at the origin)
1) L(M1+M2)/2M1
2) LM1/2(M1+M2)
3) 2(M1+M2)/LM1
4) 2LM1/(M1+M2)View SolutionFour particles of masses m, 2m, 3m & 4m respectively are placed on the periphery of a circle of radius R as shown in the figure then CM of the system contains the particle is at
 View Solution
View SolutionFour particle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
 View Solution
View Solution

