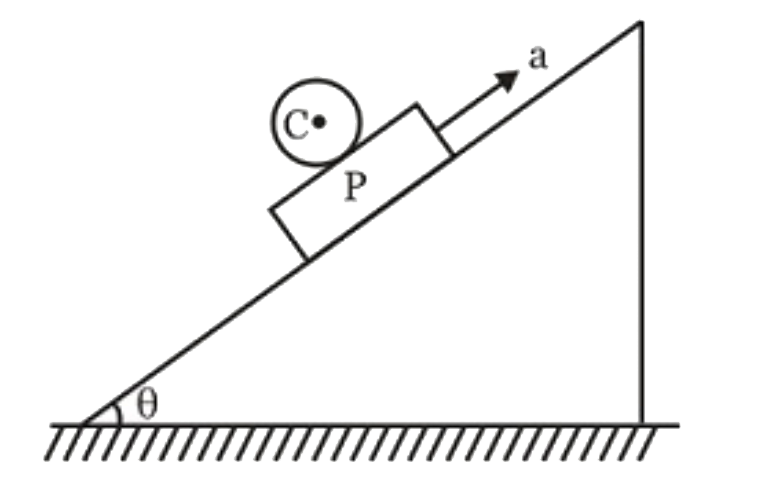
The acceleration a of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping take place between cylinder and plank)

g2sinθ
2gsinθ
gsinθ
gtanθ
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
The figure shows a fixed inclined plane on which a plank is being pulled upwards such that the center C of the solid cylinder remains at rest with respect to ground. If no slipping takes place between the cylinder and the plank, then the acceleration of the planks is
View Solution
A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View Solution
Knowledge Check
The acceleration α of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping takes place between cylinder and plank)
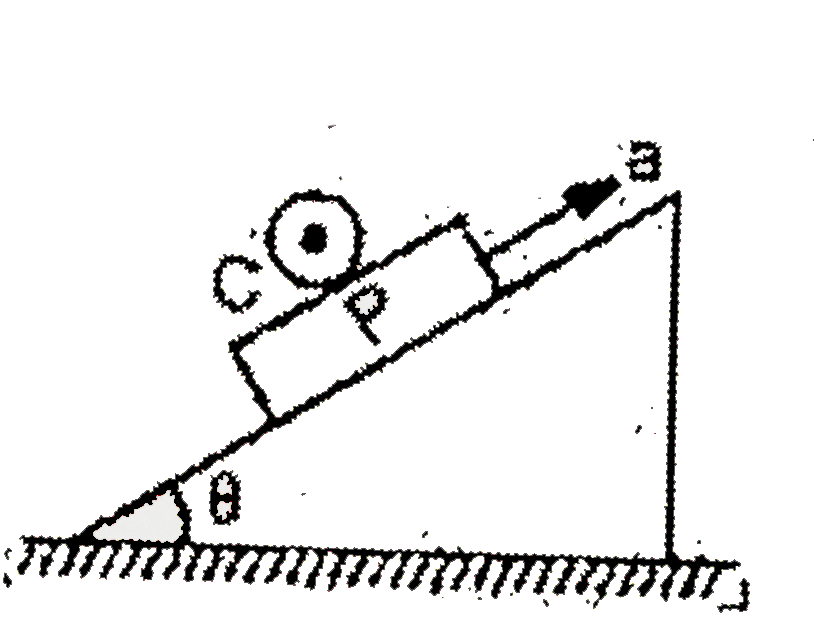 Ag2sinθB2gsinθCgsinθD√2gsinθ
Ag2sinθB2gsinθCgsinθD√2gsinθThe figure shows a fixed inclined plane on which a plank is being pulled upwards such that the center C of the solid cylinder remains at rest with respect to ground. If no slipping takes place between the cylinder and the plank, then the acceleration of the planks is
 Ag2sinθB2gsinθCgsinθD√2gsinθ
Ag2sinθB2gsinθCgsinθD√2gsinθA cylinder of mass M and radius R lies on a plank of mass M as shown. The surface between plank and ground is smooth, and between cylinder and plank is rough. Assuming no slipping between cylinder and plank, the time period of oscillation (When displaced from equilibrium) of the system is
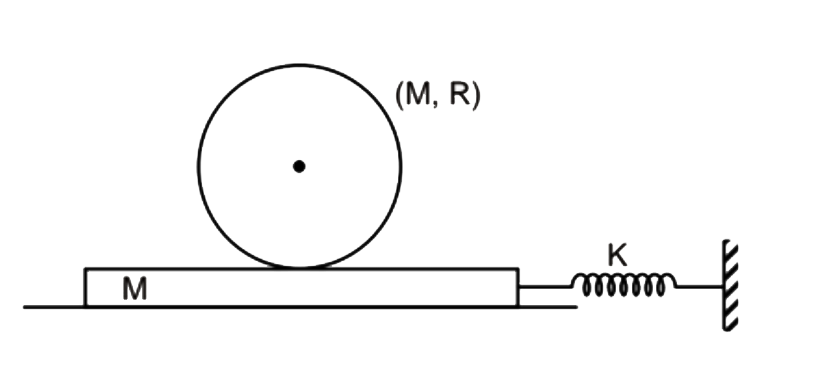 A2π√m3kB4π√2m3kC4π√M3kD4π√3M2k
A2π√m3kB4π√2m3kC4π√M3kD4π√3M2k

A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
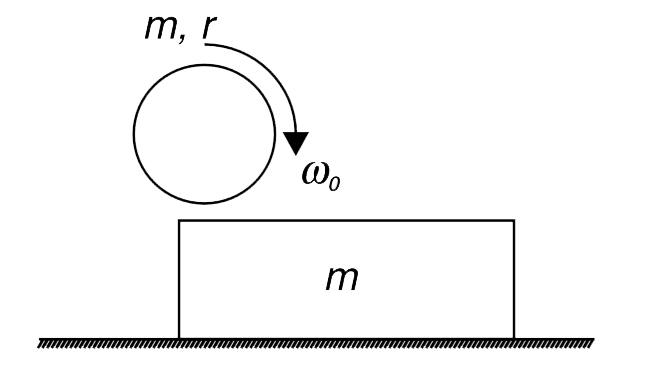
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View SolutionComprehension A solid cylinder of mass mis rotating brought in contact with a plank of ma cylinder and plank because of which there is no slipping between cylinder and plank m is rotating with angular velocity foxy about its fixed axis of symmetry. It is at with a plank of mass m placed on a smooth om a smooth surface. There exist friction between se of which plank starts moving. After some time plank moves.such that in friction does the work m Rough surface 7772 ZEITEN Smooth surface The final velocity of the plank when there is no slipping between cylinder and plank is: (0) Ros Roo 3RW (A) 2Roo Roo (B) 4
View SolutionA cylinder of mass M and radius R lies on a plank of mass M as shown. The surface between plank and ground is smooth, and between cylinder and plank is rough. Assuming no slipping between cylinder and plank, the time period of oscillation (When displaced from equilibrium) of the system is

View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View Solution
