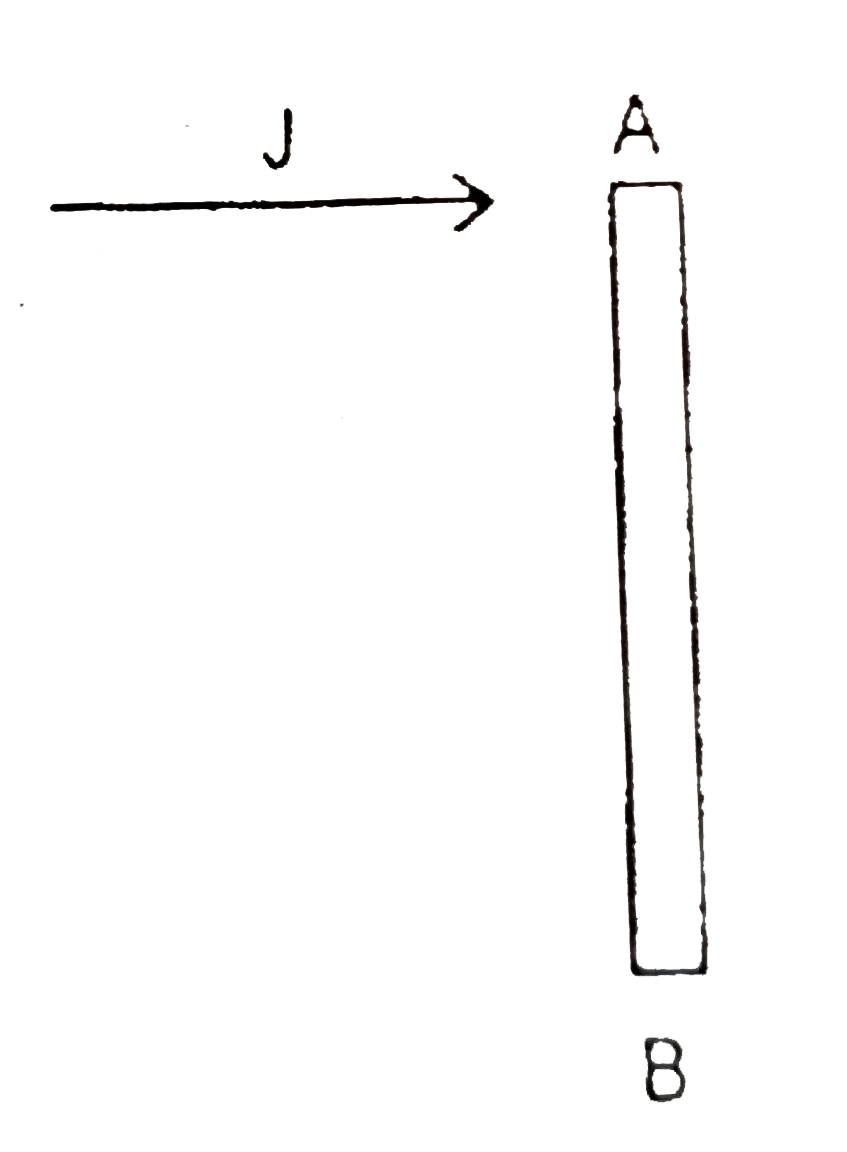
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact is
23 m
13 m
12 m
14m
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

Co-ordinates of point A of the rod after time t=π45 s will be
View SolutionOn a smooth horizontal plane, a rod PQ of length 6m and mass 2kg is placed. The centre of the rod is placed at the origin of the coordinate axes. An impulse of 4N−S is applied at P perependicular to the length of the rod. Find the distance of a point form centre of the rod which is at rest after the impact (in metres)
View Solution
Knowledge Check
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

Co-ordinates of point A of the rod after time t=π45 s will beA[(π9+√32)m,12m]B[34m32m]C[(π6+12)m,12m]D[12m,12m]A rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
 AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.
AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.A uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the magnitude of the impulse applied by the during the time interval △tAmJ(m+3M)BmJ(3m+M)CMJ(m+3M)DMJ(3m+M)
A uniform rod of length L and mass M, is lying on a frictionless horizontal plane and is pivoted at one of its ends, as shown in the figure. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and the impulse J acts for a small time interval Δt.
(a) Find with resulting instantaneous angular velocity of the rod just after the impusle is imparted.
(b) Find the impulse acted on the ball during the time interval Δt.
(c ) Find the magnitude and direction of the impulse applied by the pivot during the time interval Δt.

View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the magnitude of the impulse applied on the pivot during the time interval △t
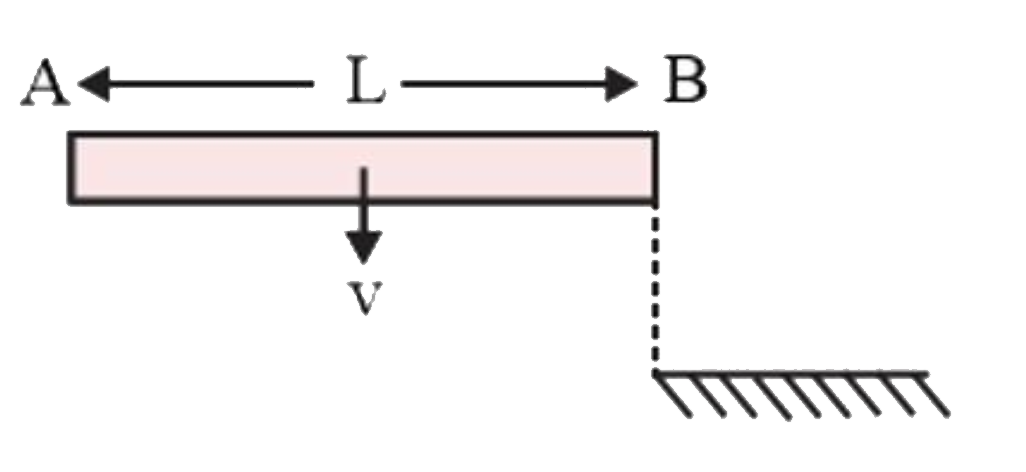
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View Solution
