A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

Co-ordinates of point A of the rod after time t=π45 s will be
[(π9+√32)m,12m]
[34m32m]
[(π6+12)m,12m]
[12m,12m]
The correct Answer is:A
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact is
View SolutionOn a smooth horizontal plane, a rod PQ of length 6m and mass 2kg is placed. The centre of the rod is placed at the origin of the coordinate axes. An impulse of 4N−S is applied at P perependicular to the length of the rod. Find the distance of a point form centre of the rod which is at rest after the impact (in metres)
View Solution
Knowledge Check
A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact isA23 mB13 mC12 mD14mA rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
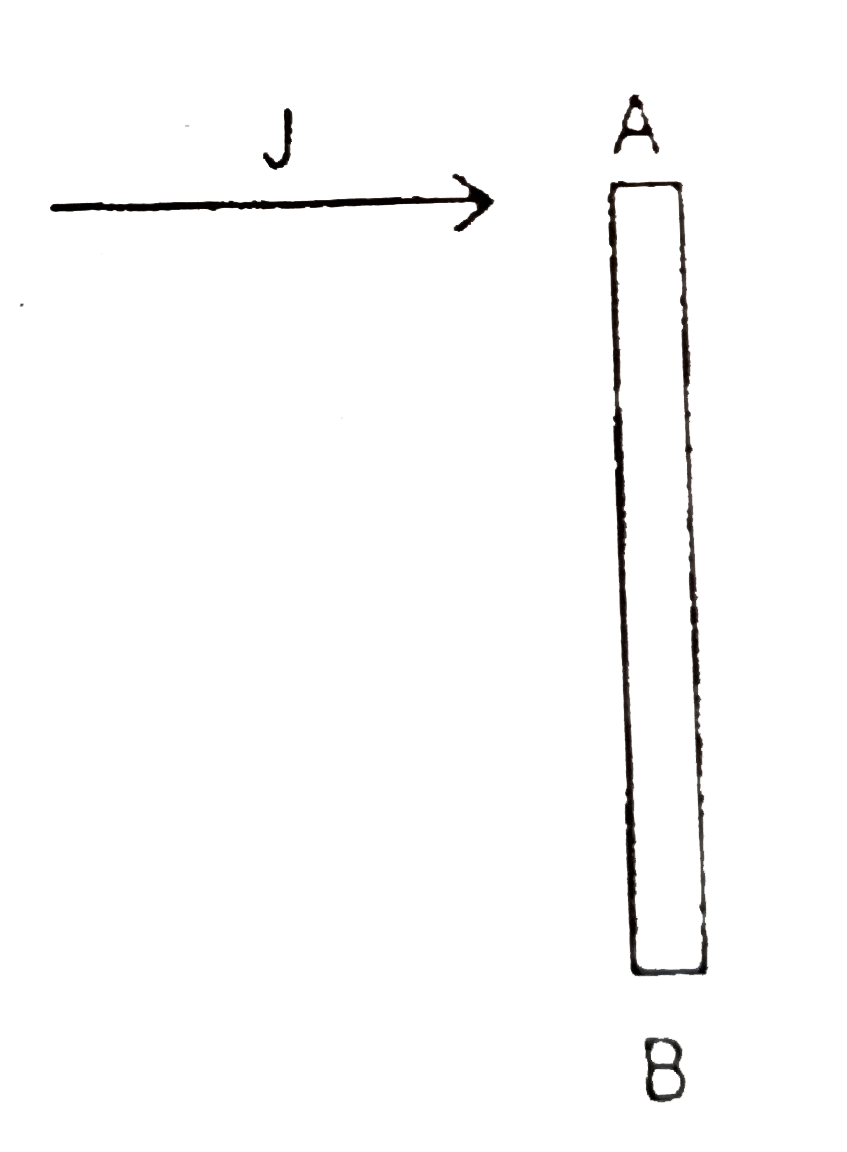 AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.
AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.A uniform rod of mass m and length l is placed over a smooth horizontal surface along the y-axis and is at rest as shown in Fig. An impulsive force F is applied for a small time △t along x-direction at point A. The x-coordinate of end A of the rod when the rod becomes parallel to x-axis for the first time is [initially, the coordinate of centre of mass of the rod is (0,0)]
 Aπl12Bl2(1+π12)C12(1−π6)Dl2(1+π6)
Aπl12Bl2(1+π12)C12(1−π6)Dl2(1+π6)
A uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
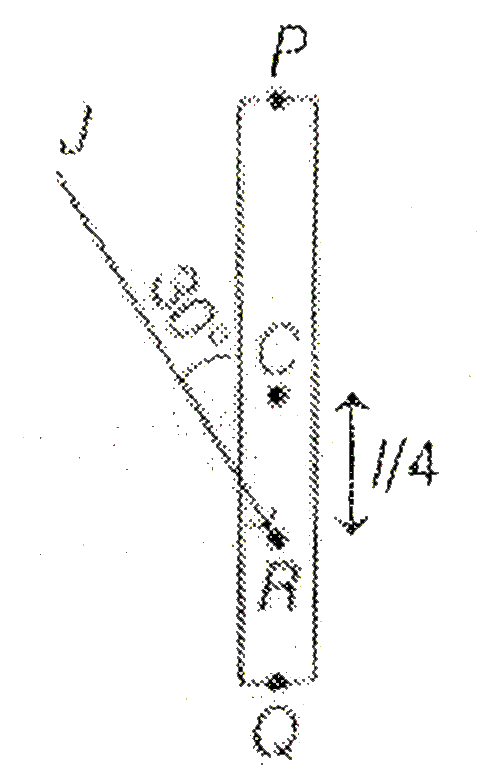
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:

View SolutionA uniform rod of length L and mass M, is lying on a frictionless horizontal plane and is pivoted at one of its ends, as shown in the figure. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and the impulse J acts for a small time interval Δt.
(a) Find with resulting instantaneous angular velocity of the rod just after the impusle is imparted.
(b) Find the impulse acted on the ball during the time interval Δt.
(c ) Find the magnitude and direction of the impulse applied by the pivot during the time interval Δt.

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View Solution
