two point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

Potential at point C
VC=Vq1+Vq2=K(2μC)6+K(−4μC)2=9×109×2×10−66−9×109×4×10−62=−15000V.
Similarly, VD=Vq1+Vq2=K(2μC)√(√5)2+22+K(−4μC)√(√5)2+22=K(2μC)3+K(−4μC)3=−6000V.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Two point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionConsider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionConsider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Charge q is
View SolutionConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Frequency of oscillation is
View SolutionConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Amplitude of motion is
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionTwo point charges 4muC and -4muC are placed at a distance 1.5 m. Total number of points except infinity, where potential due to system of charges is zero?
View Solution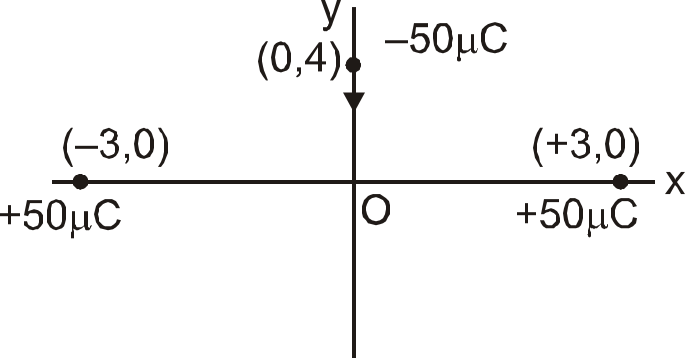
The figure shows two equal, positive charges, each of magnitude50μC, fixed at points (3, 0) m and (–3, 0)m respectively. A charge –50μC, moving along negative y–axis has a kinetic energy of 4J at the instant it crosses point (0,4)m. Determine the position of this charge where the direction of its motion reverses for the first time after crossing this point (neglect gravity).
View Solution
