Two blocks of mass 2 kg and 5 kg are connected by an ideal string passing over a pulley. The block of mass 2 kg is free to slide on a surface inclined at an angle of 30∘ with the horizontal whereas 5 kg block hangs freely. Find the acceleration of the system and the tension in the string. Given μ=0.30.
To solve the problem, we will analyze the forces acting on both blocks and use Newton's second law to find the acceleration of the system and the tension in the string.
Step 1: Identify the forces acting on each block
1. Block 1 (2 kg on the incline):
- Weight (W1) = m1 * g = 2 kg * 9.81 m/s² = 19.62 N
- Component of weight parallel to incline (W1_parallel) = W1 * sin(30°) = 19.62 N * 0.5 = 9.81 N
- Component of weight perpendicular to incline (W1_perpendicular) = W1 * cos(30°) = 19.62 N * (√3/2) ≈ 16.97 N
- Normal force (N) = W1_perpendicular = 16.97 N
- Frictional force (F_friction) = μ * N = 0.30 * 16.97 N ≈ 5.09 N
2. Block 2 (5 kg hanging):
- Weight (W2) = m2 * g = 5 kg * 9.81 m/s² = 49.05 N
Step 2: Write the equations of motion for both blocks
1. For Block 1 (2 kg):
T−W1parallel−Ffriction=m1∗a
T−9.81N−5.09N=2kg∗a
T−14.90N=2a(Equation 1)
2. For Block 2 (5 kg):
W2−T=m2∗a
49.05N−T=5kg∗a
T=49.05N−5a(Equation 2)
Step 3: Solve the equations simultaneously
Substituting Equation 2 into Equation 1:
(49.05N−5a)−14.90N=2a
49.05N−14.90N=2a+5a
34.15N=7a
a=34.15N7≈4.88m/s²
Step 4: Calculate the tension in the string
Substituting the value of a back into Equation 2:
T=49.05N−5(4.88m/s²)
T=49.05N−24.4N≈24.65N
Final Results
- The acceleration of the system a is approximately 4.88m/s².
- The tension in the string T is approximately 24.65N.
---
- Weight (W1) = m1 * g = 2 kg * 9.81 m/s² = 19.62 N
- Component of weight parallel to incline (W1_parallel) = W1 * sin(30°) = 19.62 N * 0.5 = 9.81 N
- Component of weight perpendicular to incline (W1_perpendicular) = W1 * cos(30°) = 19.62 N * (√3/2) ≈ 16.97 N
- Normal force (N) = W1_perpendicular = 16.97 N
- Frictional force (F_friction) = μ * N = 0.30 * 16.97 N ≈ 5.09 N
- Weight (W2) = m2 * g = 5 kg * 9.81 m/s² = 49.05 N
T−W1parallel−Ffriction=m1∗a
T−9.81N−5.09N=2kg∗a
T−14.90N=2a(Equation 1)
W2−T=m2∗a
49.05N−T=5kg∗a
T=49.05N−5a(Equation 2)
(49.05N−5a)−14.90N=2a
49.05N−14.90N=2a+5a
34.15N=7a
a=34.15N7≈4.88m/s²
T=49.05N−5(4.88m/s²)
T=49.05N−24.4N≈24.65N
- The tension in the string T is approximately 24.65N.
Topper's Solved these Questions
- LAWS OF MOTION : FRICTIONBOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Problems
17 Videos
- LAWS OF MOTION : FRICTIONBOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Self Practice
95 Videos
- Laws of MotionBOOK - SL ARORACHAPTER - Laws of MotionEXERCISE - Exercise
627 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
Similar Questions
Two blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles 30∘ and 60∘ resp . With horizontal .Determine the accelertion in the two blocks and tension in the string g=10m/s2 .
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
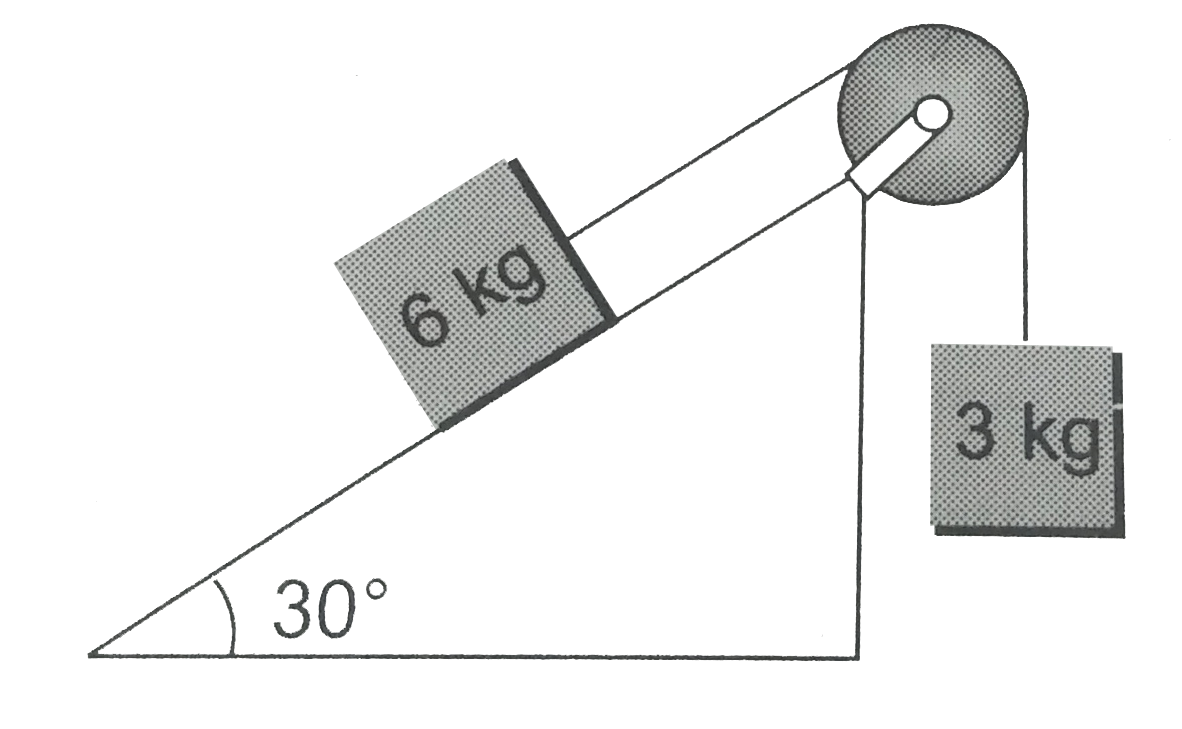 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2Two masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is
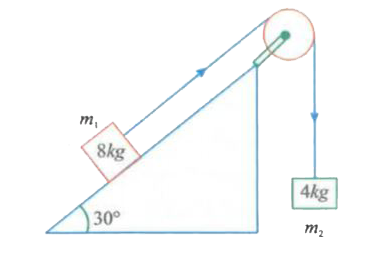 A4m/s2B2m/s2CzeroD9.8m/s2
A4m/s2B2m/s2CzeroD9.8m/s2
A block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionTwo blocks of masses 2.0 kg and 3.0 kg are connected by light inextensible string. The string passes ove an ideal pulley pivoted to a fixed axel on a smooth incline place as shown in the figure. When the blocks are released, find magnitude of their accelerations.

View SolutionA block of mass 10 kg is sliding on a surface inclined at 30∘ with horizontal . If coefficient of friction between the block and the surface is 0.5 , find acceleration produced in the block . Take g=9.8m/2 .
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionTwo masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is

View Solution
