A bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
0.5 kPa
1 kPa
5kPa
None of these
The correct Answer is:B
To find the water pressure above atmospheric pressure at the bottom of the bucket, we can follow these steps:
Step 1: Understand the System
The bucket is filled with water to a height of 15 cm. The bucket is tied to a rope that passes over a frictionless pulley, and the other end of the rope is tied to a weight that is half the mass of the bucket plus the mass of the water.
Step 2: Define the Variables
Let:
- m = mass of the bucket + mass of the water
- h = height of the water = 15 cm = 0.15 m
- g = acceleration due to gravity = 9.81 m/s²
Step 3: Calculate the Effective Weight
The weight acting on the system due to the mass hanging from the rope is:
W=m2⋅g
The effective force acting on the bucket due to the weight is:
Fnet=m⋅g−m2⋅g=m2⋅g
Step 4: Calculate the Acceleration
Using Newton's second law, we can find the acceleration of the system:
Fnet=(m+m2)⋅a
m2⋅g=3m2⋅a
Solving for a:
a=g3
Step 5: Determine the Pressure at the Bottom of the Bucket
The pressure at the bottom of the bucket due to the water column is given by:
P=ρ⋅g⋅h
Where ρ is the density of water (approximately 1000kg/m3). Therefore, substituting the values:
P=1000⋅9.81⋅0.15
Calculating this gives:
P=1471.5Pa
Step 6: Calculate the Water Pressure Above Atmospheric Pressure
The water pressure above atmospheric pressure is:
Pabove=P−Patmospheric
Since atmospheric pressure is not included in this calculation, we can consider the pressure calculated as the gauge pressure:
Pabove=1471.5Pa≈1.47kPa
Final Answer
The water pressure above atmospheric pressure at the bottom of the bucket is approximately 1.47 kPa.
---
The bucket is filled with water to a height of 15 cm. The bucket is tied to a rope that passes over a frictionless pulley, and the other end of the rope is tied to a weight that is half the mass of the bucket plus the mass of the water.
Let:
- m = mass of the bucket + mass of the water
- h = height of the water = 15 cm = 0.15 m
- g = acceleration due to gravity = 9.81 m/s²
The weight acting on the system due to the mass hanging from the rope is:
W=m2⋅g
The effective force acting on the bucket due to the weight is:
Fnet=m⋅g−m2⋅g=m2⋅g
Using Newton's second law, we can find the acceleration of the system:
Fnet=(m+m2)⋅a
m2⋅g=3m2⋅a
Solving for a:
a=g3
The pressure at the bottom of the bucket due to the water column is given by:
P=ρ⋅g⋅h
Where ρ is the density of water (approximately 1000kg/m3). Therefore, substituting the values:
P=1000⋅9.81⋅0.15
Calculating this gives:
P=1471.5Pa
The water pressure above atmospheric pressure is:
Pabove=P−Patmospheric
Since atmospheric pressure is not included in this calculation, we can consider the pressure calculated as the gauge pressure:
Pabove=1471.5Pa≈1.47kPa
The water pressure above atmospheric pressure at the bottom of the bucket is approximately 1.47 kPa.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct21videos
PROPERTIES OF MATTER
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension32videos
PROPERTIES OF MATTER
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.15videos
RAY OPTICS
Similar Questions
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket.
View SolutionA monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.View Solution
Knowledge Check
- Question 1 - Select One
A bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
A0.5 kPaB1 kPaC5 kPaD20 kPa - Question 2 - Select One
A cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope where the cat move upwards with in acceleration a=2m/s2 relative to the rope ?
 A2 NB12NC8ND4N
A2 NB12NC8ND4N - Question 3 - Select One
A body of mass 10 kg is placed on the horizontal smooth table (see given figure). A string is tied with it which passes over a frictionless pulley. The other end of the string is tied with a body of mass 5 kg. When the bodies move, the acceleration produced in them, is
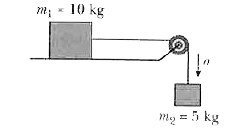 A9.8 m/s2B4.8 m/s2C4.25 m/s2D3.27 m/s2
A9.8 m/s2B4.8 m/s2C4.25 m/s2D3.27 m/s2
A monkey of massm clings to a rope slung over a fixed pulley. The opposite end of the rope is tied to a weight of
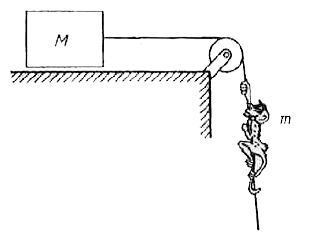
mass M lying on a horizontal plat (Fig.). Neglecting friction find the acceleration of both bodies (relative to the plate) and the tension of the rope for the three cases:
(1) the monkey does not move with respect to the rope,
(2) the monkey moves upwards with respect to the rope with acceleration b,
(3) the monkey moves downwards with respect to the rope with an acceleration b.View SolutionA bucket of water tied to one end of a rope of length 3 m is rotated in a vertical circle about the other end in such a way that water in it dows not spill . Calculate the minimum velocity of the bucket at which this happens .
View SolutionA person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 View Solution
View SolutionA man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
View Solution

