The position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The total distance travelled by the paticle between t=0 to t=1s is
0m
1m
2m
12m
The correct Answer is:B
To find the total distance travelled by the particle between t=0 seconds and t=1 second, we start with the position function given by:
x(t)=2(t−t2)
Step 1: Determine the position at t=0 seconds.
Substituting t=0 into the position function:
x(0)=2(0−02)=2(0)=0 meters
Step 2: Determine the position at t=1 second.
Substituting t=1 into the position function:
x(1)=2(1−12)=2(1−1)=2(0)=0 meters
Step 3: Find the position at t=12 seconds to check for maximum displacement.
Substituting t=12 into the position function:
x(12)=2(12−(12)2)=2(12−14)=2(14)=12 meters
Step 4: Analyze the motion of the particle.
From t=0 to t=12 seconds, the particle moves from 0 meters to 12 meters.
From t=12 seconds to t=1 second, the particle moves back from 12 meters to 0 meters.
Step 5: Calculate the total distance travelled.
The total distance travelled is the sum of the distances in both segments of the motion:
1. Distance from 0 to 12 meters: 12 meters
2. Distance from 12 meters back to 0 meters: 12 meters
Thus, the total distance travelled is:
Total Distance=12+12=1 meter
Final Answer:
The total distance travelled by the particle between t=0 seconds and t=1 second is 1 meter.
---
Substituting t=0 into the position function:
Substituting t=1 into the position function:
Substituting t=12 into the position function:
From t=0 to t=12 seconds, the particle moves from 0 meters to 12 meters.
The total distance travelled is the sum of the distances in both segments of the motion:
2. Distance from 12 meters back to 0 meters: 12 meters
The total distance travelled by the particle between t=0 seconds and t=1 second is 1 meter.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
Match the following Table-1 to Table-2

View SolutionA stone is dropped form certain height which can reach the ground in 5s. If the stone is stopped after 3s of its fall and then allowed to fall again. Find the time taken (in second) by the stone to reach the ground for the remaining distance.
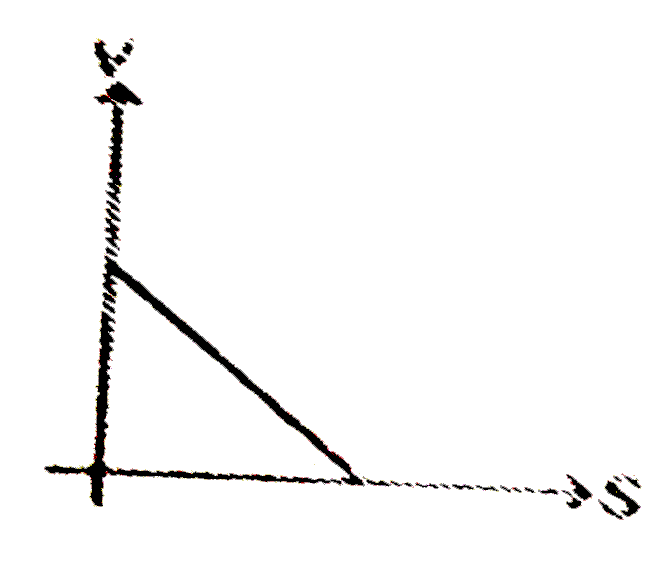
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
View SolutionA particle is projected with velocity 2(√gh), so that it just clears two walls of equal height h which are at a distance of 2h form each other. Show that the time of passing between the walls is 2(√hg). [Hint : First find velocity at height h. Treat it as initial velocity and 2h as the range. ]
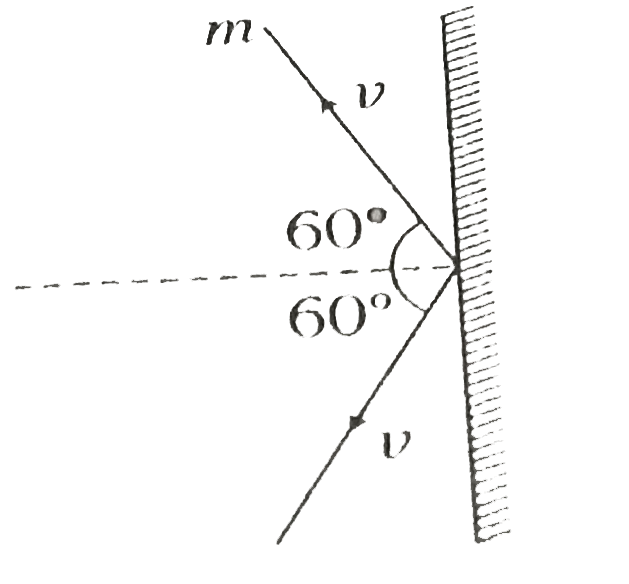
View SolutionA rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The acceleration of the particle is
View SolutionThe position of a particle is given by x=2(t-t^(2)) where t is expressed in seconds and x is in metre. The maximum value of position co-ordinate of particle on positive x -axis is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The particle
View SolutionThe position of a particle is given by x=2(t-t^(2)) where t is expressed in seconds and x is in metre. When is the object at rest?
View SolutionThe distance travelled s in metres by a particle in t second is given by s=t3+2t2+t. The speed of the particle after 1s will be
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t +3t^(2) -t^(3) , where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe displacement of a particle is given by x = (t-2)^(2) where x is in metre and t in second. The distance covered by the particle in first 4 seconds is
View Solutionx-अक्ष के अनुदिश गतिशील कण की स्थिति x=2+8t−4t2 द्वारा व्यक्त की जाती है। t = 0 से t = 2 तक कण के द्वारा तय दूरी होगी -
View SolutionThe displacement of a particle is given by x=(t−2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is
View SolutionThe displacement of a particle is given by x=(t−2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is
View Solution
