Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
ϕ
34πϕ
2π3ϕ
4π3ϕ
The correct Answer is:D
To solve the problem, we need to determine the net electric flux passing through the surface of an imaginary sphere of radius a when the net flux through an imaginary cube of side a is given as ϕ.
1. Understanding Electric Flux:
Electric flux (Φ) through a closed surface is defined by Gauss's Law:
Φ=Qencϵ0
where Qenc is the total charge enclosed within the surface and ϵ0 is the permittivity of free space.
2. Flux through the Cube:
Given that the net flux through the surface of the cube of side a is ϕ, we can express this as:
ϕ=Qenc, cubeϵ0
This implies that the charge enclosed by the cube is:
Qenc, cube=ϕ⋅ϵ0
3. Charge Density:
If we assume that the charge is uniformly distributed in space, we can define the charge density ρ as:
ρ=Qenc, cubeVcube
where Vcube=a3 is the volume of the cube. Thus,
ρ=Qenc, cubea3=ϕ⋅ϵ0a3
4. Flux through the Sphere:
Now, we need to find the flux through a sphere of radius a. The volume of the sphere is given by:
Vsphere=43πa3
The charge enclosed by the sphere can be calculated as:
Qenc, sphere=ρ⋅Vsphere=(ϕ⋅ϵ0a3)⋅(43πa3)
Simplifying this gives:
Qenc, sphere=43πϕ⋅ϵ0
5. Calculating the Flux through the Sphere:
Now we can find the flux through the sphere using Gauss's Law:
Φsphere=Qenc, sphereϵ0=43πϕ⋅ϵ0ϵ0=43πϕ
Thus, the net flux passing through the surface of the imaginary sphere of radius a is:
Φsphere=43πϕ
Final Answer:
The net flux passing through the surface of the imaginary sphere of radius a is 43πϕ.
Electric flux (Φ) through a closed surface is defined by Gauss's Law:
Φ=Qencϵ0
where Qenc is the total charge enclosed within the surface and ϵ0 is the permittivity of free space.
Given that the net flux through the surface of the cube of side a is ϕ, we can express this as:
ϕ=Qenc, cubeϵ0
This implies that the charge enclosed by the cube is:
Qenc, cube=ϕ⋅ϵ0
If we assume that the charge is uniformly distributed in space, we can define the charge density ρ as:
ρ=Qenc, cubeVcube
where Vcube=a3 is the volume of the cube. Thus,
ρ=Qenc, cubea3=ϕ⋅ϵ0a3
Now, we need to find the flux through a sphere of radius a. The volume of the sphere is given by:
Vsphere=43πa3
The charge enclosed by the sphere can be calculated as:
Qenc, sphere=ρ⋅Vsphere=(ϕ⋅ϵ0a3)⋅(43πa3)
Simplifying this gives:
Qenc, sphere=43πϕ⋅ϵ0
Now we can find the flux through the sphere using Gauss's Law:
Φsphere=Qenc, sphereϵ0=43πϕ⋅ϵ0ϵ0=43πϕ
Φsphere=43πϕ
The net flux passing through the surface of the imaginary sphere of radius a is 43πϕ.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
AϕB34πϕC2π3ϕD4π3 phiA charge Q is situated at the corner of a cube, the electric flux passing through all the six faces of the cube is :
AQ6ε0BQ8ε0CQε0DQ2ε0If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
A0Bsame at all placesCdepends upon the location of pointsDinfinite
A chrage 'q' is placed at the centre of a cube of side 'l' . What is the electric flux passing through each face of the cube?
View SolutionWhen a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View SolutionA point charge Q is placed at the centre of a hemisphere. Find the electric flux passing through flat surface of hemisphere.
View SolutionA charge Q is situated at the corner of a cube the electric flux passed through all the six faces of the cube is :
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
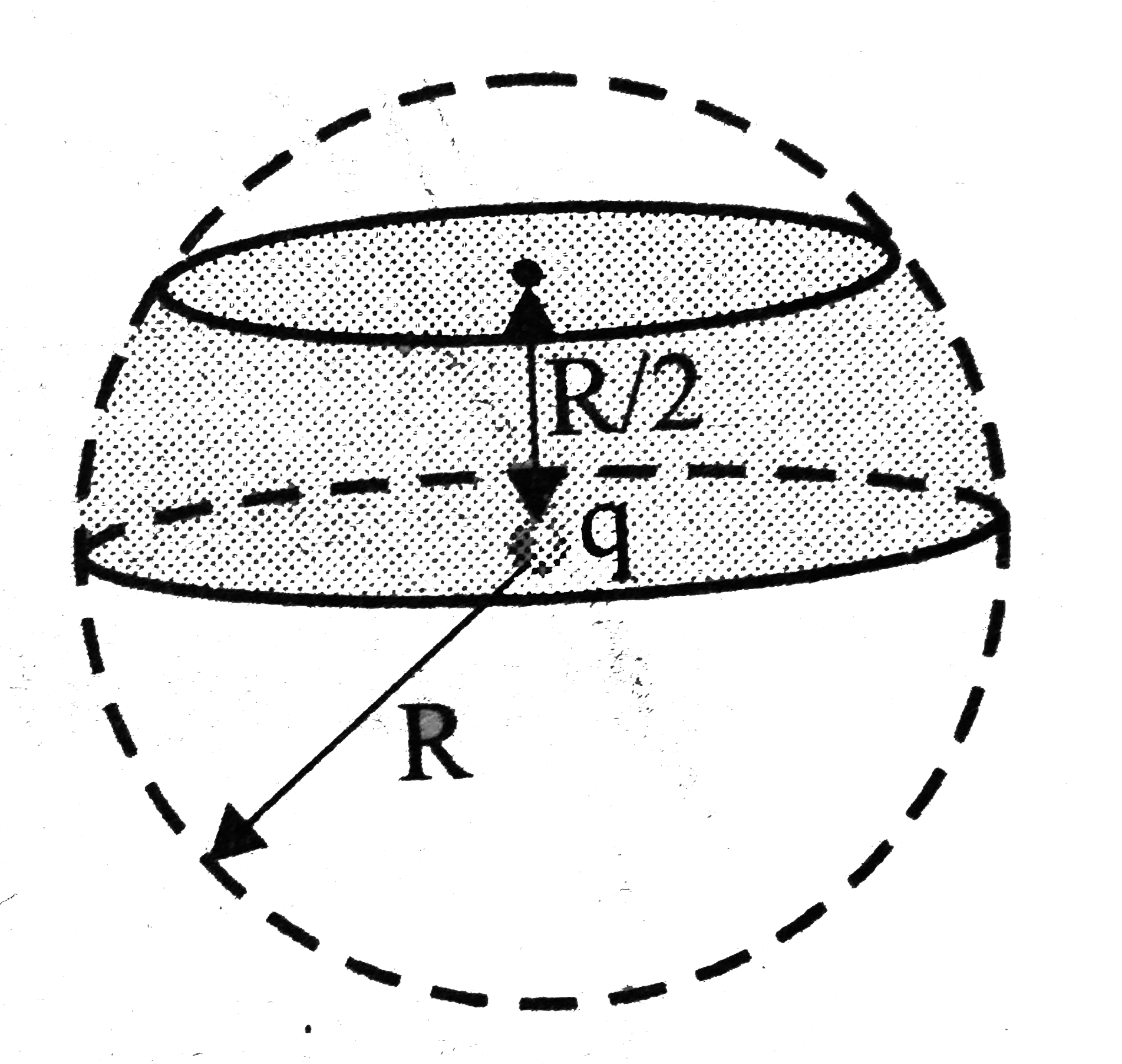
View Solution
