A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is
μ0IπR(tanπn)
μ0I4πR(tanπn)
μ0I2πR(tanπn)
μ0I2πR(cosπn)
The correct Answer is:C
Step by step video & image solution for A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
Aμ0IπR(tanπn)Bμ0I4πRtanπnCμ0I2πR(tanπn)Dμ0I2πR(cosπn)In the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
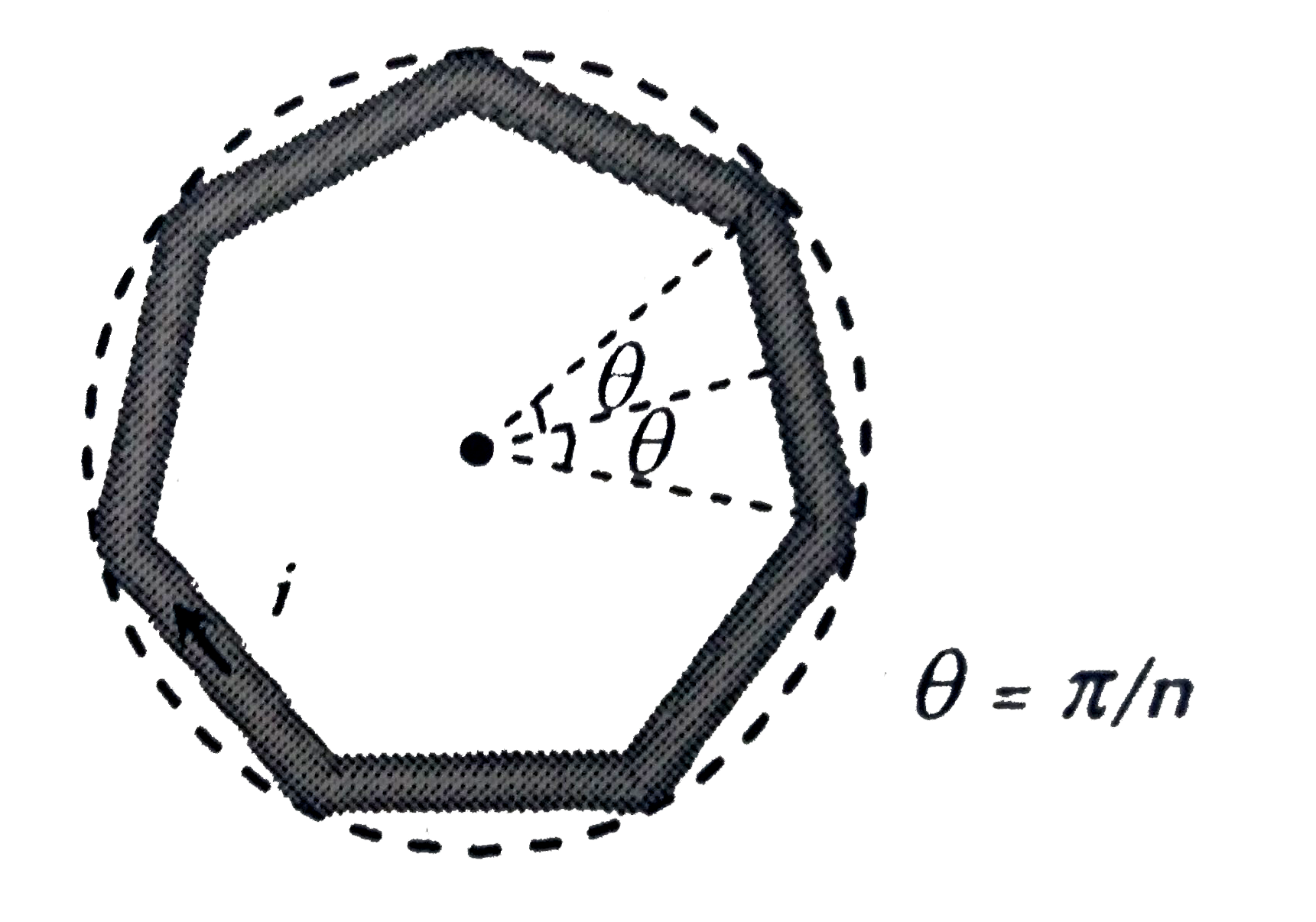 Aμ0i2πatanπnBμ0ni2πatanπnC2πniaμ0tanπnDni2aμ0tanπn
Aμ0i2πatanπnBμ0ni2πatanπnC2πniaμ0tanπnDni2aμ0tanπnA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when n→∞ is (R is the radius of its circumcircle)
Aμ0ni2πRtanπ6Bμ0ni2πRtanπRCμ0i2RDzero
A regular polygon of 9 sides where length of each side is 2 is inscribed in a circle. Then the radius of the circle is
View SolutionIf a twelve sides regular polygon is inscribed in a circle of radius 3 centimeters, then the length of each side of the polygon is
View SolutionIf a thin wire of length L is given the shape of a regular polygon of n sides and current I flows through it, what will be the net magnetic field at the centre of the polygon if n is infinity?
View SolutionThe limit of the interior angle of a regular polygon of n sides as n→∞ is
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View Solution
