Find the expession for the equivalent emf & internal resistanceof the series combination of cells.
(i) Suppose n cells, each of emf ξ volts and internal resistance r ohms are connected in series with an external resistance R.

(ii) The total emf of the battery nξ
The total resistance in the circuit nr+R by Ohm's law, the currentin the circuit is
I=total emftotal resistance=nξnr+R
Case (a) if r<<R, then,
I=nξR≈nI1
(iii) Where I1 is the current due to a single cell (I1=ξR)
Thus, if r is negligible when comparedto R the current supplied by the battery is n times that supplied by a single cell.
Case (b) If r<<R,I=nξnr≈ξr
(iv) It is the current due to a single cell. That is , current due to the whole battery is the same as that due to a single cell and hence there is no advantage in connecting several cells.
(v) Thus series connection of cells is advantageous only when the effective internal resistanceof the cell is negaligibly small compared with R.
Similar Questions
Two cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View Solution
Knowledge Check
Six cell each of emf E and internal resistance r are connected in series. If due to over sight, two cells are connected wrongly, then the equivalent emf and internal resistance of the combination is
A6E,6rB4E,6rC2E,6rD2E,4rFour identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
A2E and 4rB4E and 4rC2E and 2rD4E and 2rFive cells each of emf E and internal resistance r are connected in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
A3E,3rB5E , 3rC3E, 5rD5E,5r
Four identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View SolutionFind the equivalent emf and internal resistance of the arrangement shown in figure.
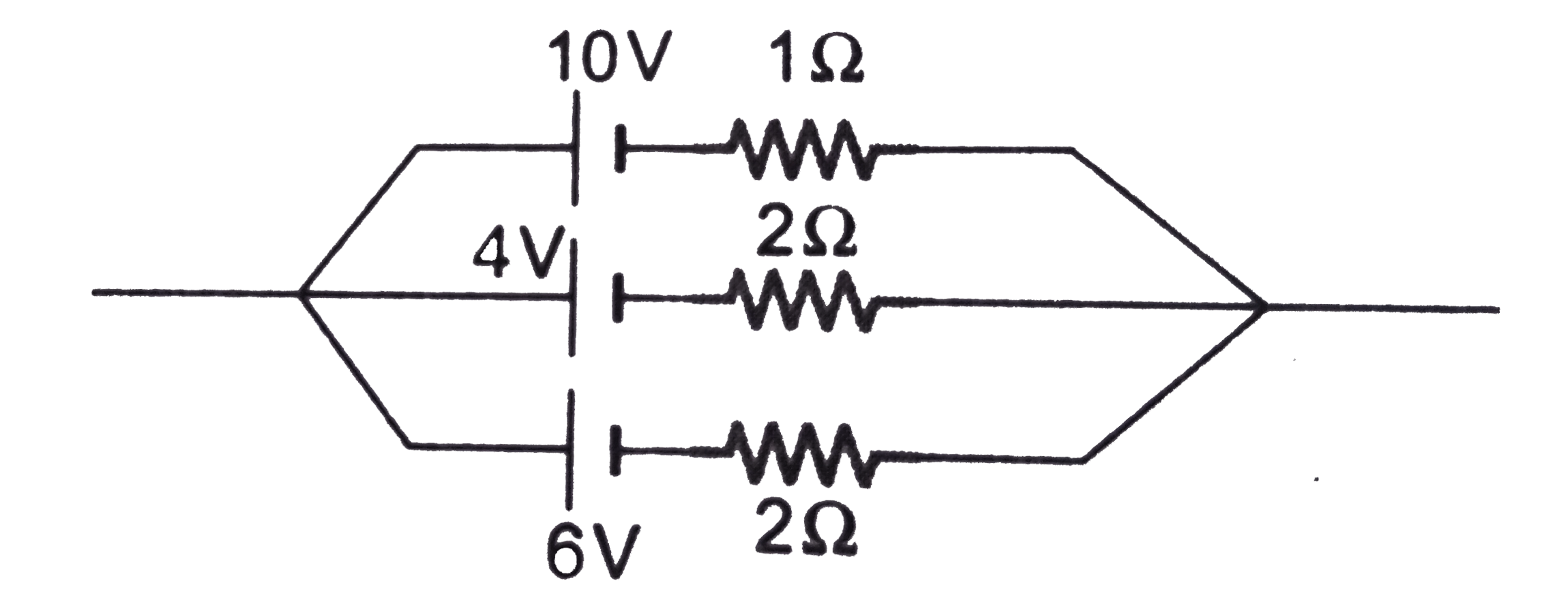
View SolutionFind the equivalent emf and internal resistance of the arrangement shown in figure.

View SolutionTwo cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

View SolutionThe equivalent resistance in series combination is
View Solution
