Four identical cells of emf and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
2E and 4r
4E and 4r
2E and 2r
4E and 2r
The correct Answer is:A
To solve the problem, we need to determine the equivalent EMF and effective internal resistance when four identical cells, each with an EMF of ϵ and an internal resistance of r, are connected in series, with one cell connected in the reverse direction.
1. Identify the Configuration:
We have four cells connected in series. Three cells are connected in the correct orientation, while one cell is connected in the reverse direction.
2. Calculate the Equivalent EMF:
- The EMF of each of the three correctly connected cells is ϵ.
- The EMF of the incorrectly connected cell is −ϵ (since it opposes the current).
- Therefore, the total equivalent EMF Eeq can be calculated as:
Eeq=ϵ+ϵ+ϵ−ϵ=3ϵ−ϵ=2ϵ
3. Calculate the Effective Internal Resistance:
- The internal resistance of each cell is r.
- When cells are connected in series, their internal resistances add up.
- Thus, the total internal resistance Req is:
Req=r+r+r+r=4r
4. Final Result:
- The equivalent EMF of the combination is 2ϵ.
- The effective internal resistance of the combination is 4r.
Summary:
- Equivalent EMF: 2ϵ
- Effective Internal Resistance: 4r
We have four cells connected in series. Three cells are connected in the correct orientation, while one cell is connected in the reverse direction.
- The EMF of each of the three correctly connected cells is ϵ.
- The EMF of the incorrectly connected cell is −ϵ (since it opposes the current).
- Therefore, the total equivalent EMF Eeq can be calculated as:
Eeq=ϵ+ϵ+ϵ−ϵ=3ϵ−ϵ=2ϵ
- The internal resistance of each cell is r.
- When cells are connected in series, their internal resistances add up.
- Thus, the total internal resistance Req is:
Req=r+r+r+r=4r
- The equivalent EMF of the combination is 2ϵ.
- The effective internal resistance of the combination is 4r.
- Equivalent EMF: 2ϵ
- Effective Internal Resistance: 4r
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Five cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
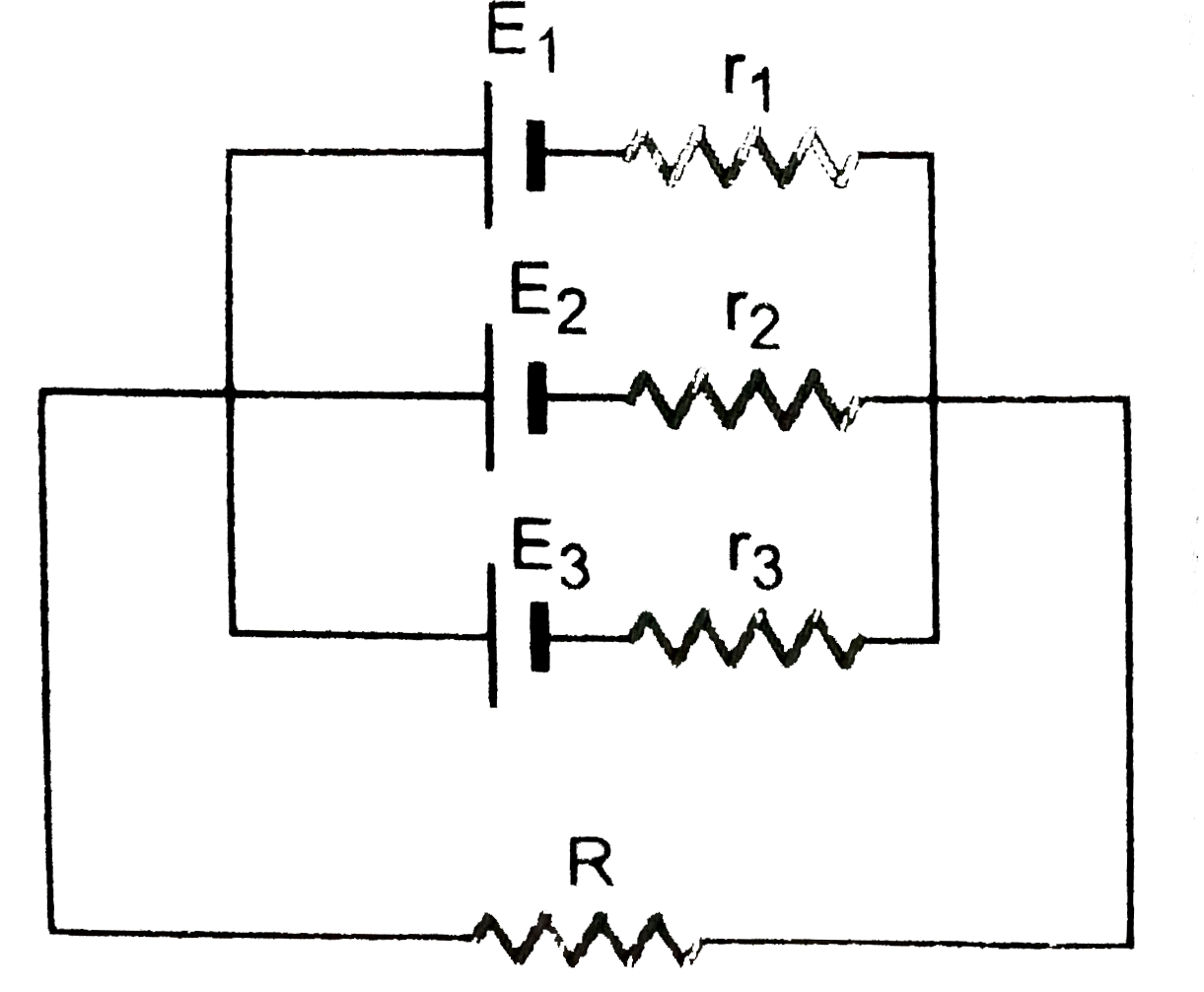
View SolutionIn a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is

View SolutionN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to form a closed cirucit. One cell A is joined with reversed polarity. The potential difference across any one cell is
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
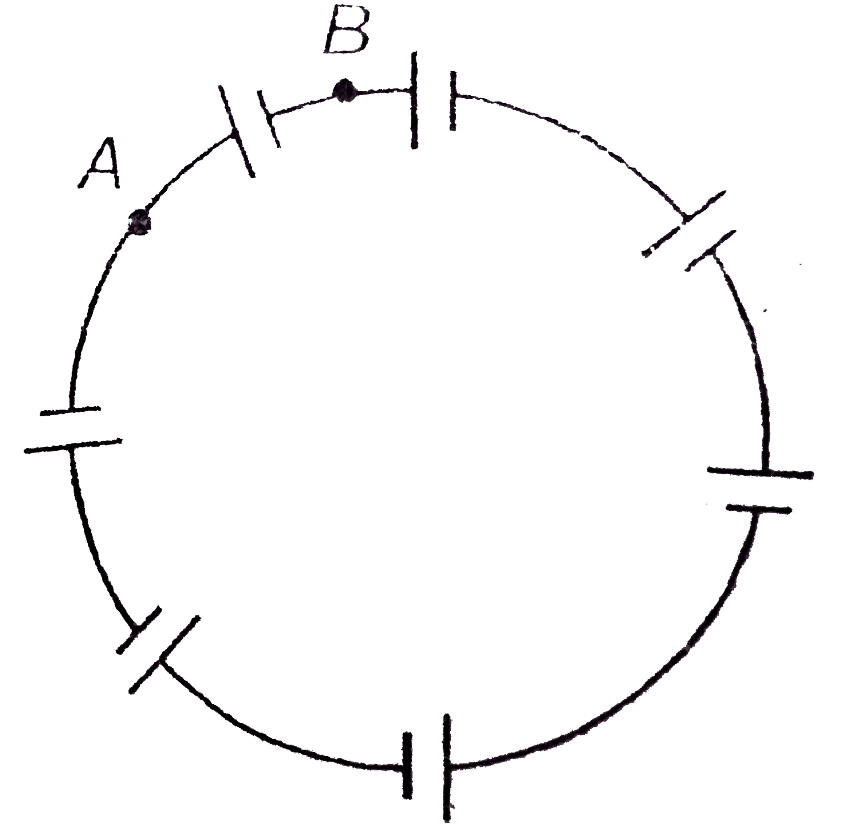
View Solution
