Five cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
3E,3r
5E , 3r
3E, 5r
5E,5r
The correct Answer is:3
To find the equivalent emf and internal resistance of the combination of five cells connected in series, with one cell connected in reverse, we can follow these steps:
Step 1: Understand the Configuration
We have five cells, each with an emf (E) and an internal resistance (r). Four cells are connected in the correct orientation, while one cell is connected in reverse.
Step 2: Calculate the Equivalent EMF
The equivalent emf (E_eq) of cells in series is the sum of their individual emfs. For the four cells connected correctly, their contribution to the emf is:
- E1 = E
- E2 = E
- E3 = E
- E4 = E
The fifth cell, which is connected in reverse, contributes negatively:
- E5 = -E
Thus, the equivalent emf can be calculated as:
Eeq=E1+E2+E3+E4+E5=E+E+E+E−E
Eeq=4E−E=3E
Step 3: Calculate the Equivalent Internal Resistance
The internal resistances of cells in series simply add up. Since all cells have the same internal resistance (r), the equivalent internal resistance (R_eq) will be:
Req=r1+r2+r3+r4+r5=r+r+r+r+r
Req=5r
Final Result
Therefore, the equivalent emf and internal resistance of the combination of the cells is:
- Equivalent EMF = 3E
- Equivalent Internal Resistance = 5r
Summary
The equivalent emf of the combination is 3E and the equivalent internal resistance is 5r.
---
We have five cells, each with an emf (E) and an internal resistance (r). Four cells are connected in the correct orientation, while one cell is connected in reverse.
The equivalent emf (E_eq) of cells in series is the sum of their individual emfs. For the four cells connected correctly, their contribution to the emf is:
- E1 = E
- E2 = E
- E3 = E
- E4 = E
- E5 = -E
Eeq=E1+E2+E3+E4+E5=E+E+E+E−E
Eeq=4E−E=3E
The internal resistances of cells in series simply add up. Since all cells have the same internal resistance (r), the equivalent internal resistance (R_eq) will be:
Req=r1+r2+r3+r4+r5=r+r+r+r+r
Req=5r
Therefore, the equivalent emf and internal resistance of the combination of the cells is:
- Equivalent EMF = 3E
- Equivalent Internal Resistance = 5r
The equivalent emf of the combination is 3E and the equivalent internal resistance is 5r.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Four identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nrIn the series combination of n cells each cell having emf ε and internal resistance r. If three cells are wrongly connected, then total emf and internal resistance of this combination will be
Anε,(nr−3r)B(nε−2r),nrC(nε−4ε),nrD(nε−6ε),nr
Ten cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
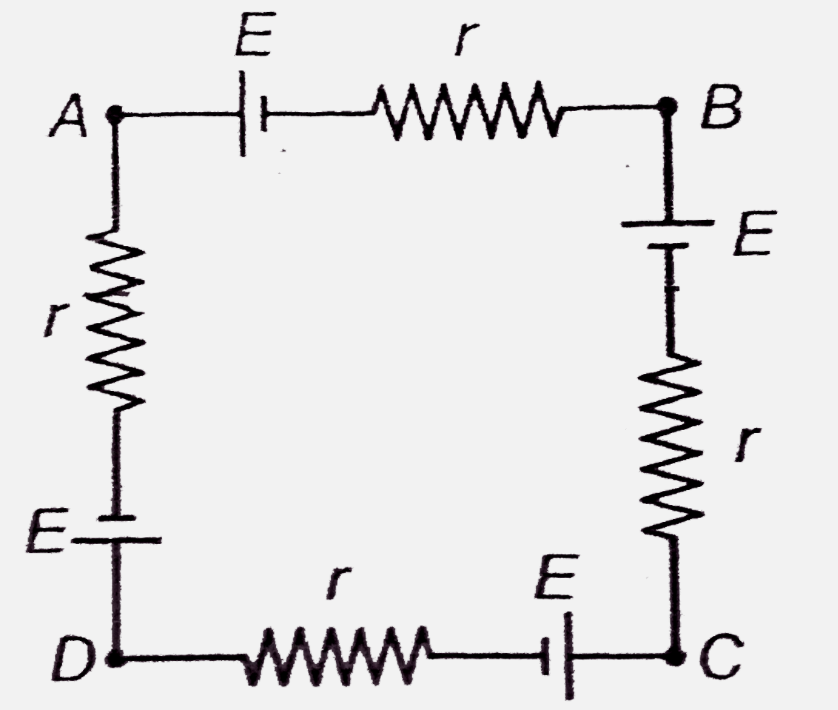
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View Solution
