State Biot - Savart's law.
The magnitude of magnetic field −→dB at a point P at a distance r from the small elemental length taken on a conductor carrying current varies
(i) directly as the strength of the current I
(ii) directly as the magnitude of the length element →dl
(iii) directly as the sine of the angle ( say , θ) between →dl and ˆr .
(iv) inversely as the square of the distance between the point P and length element →dl.
This is expressed as
dB∝Idlr2sinθ
dB=KIdlr2sinθ
where K=μ04π in SI units and K = 1 in CGS units. Is vector notation,
d→B=μ04πI→dl׈rr2
Here vector −→dB is perpendicular to both I →dl ( pointing the direction of current flow) and the unit vector ˆr directed from →dl toward point P .
Similar Questions
State Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View Solution
Knowledge Check
A: Ampere circuital law is not independent of the Biot- Savart's law.
R: Ampere's Circuital law can be derived from the Blot Savart law.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark 2.CIf assertion is true statement but Reason is false, then mark (3)DIf both Assertion and Reason are false statements, then mark (4)
(a) State Biot - Savart law and express this law in the vactor form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A
respectively, are placed concentrically and perpendicular to each other lying in the XY
and YZ planes. Find the magnitude and direction of the net magnetic field at the centre
of the coils.
View SolutionState the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View SolutionState Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element →dl at point P situated at a distance →r from the element as shown in figure.
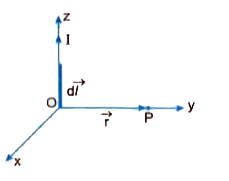
View SolutionState the Biot-Savart's law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of a circular loop of radius R carrying a steady current I, sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
View SolutionA: Ampere circuital law is not independent of the Biot- Savart's law.
R: Ampere's Circuital law can be derived from the Blot Savart law.
View SolutionState Biot-Savart law.
View SolutionState Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?
View Solution
