The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A

$\frac{2 in 2 - 1}{γ / (γ - 1)}$

B

$\frac{1 - 1 in 2}{γ / (γ - 1)}$

C

$\frac{2 in 2 + 1}{γ / (γ - 1)}$

D

$\frac{2 in 2 - 1}{γ / (γ + 1)}$

Video Solution

Text Solution

Verified by Experts

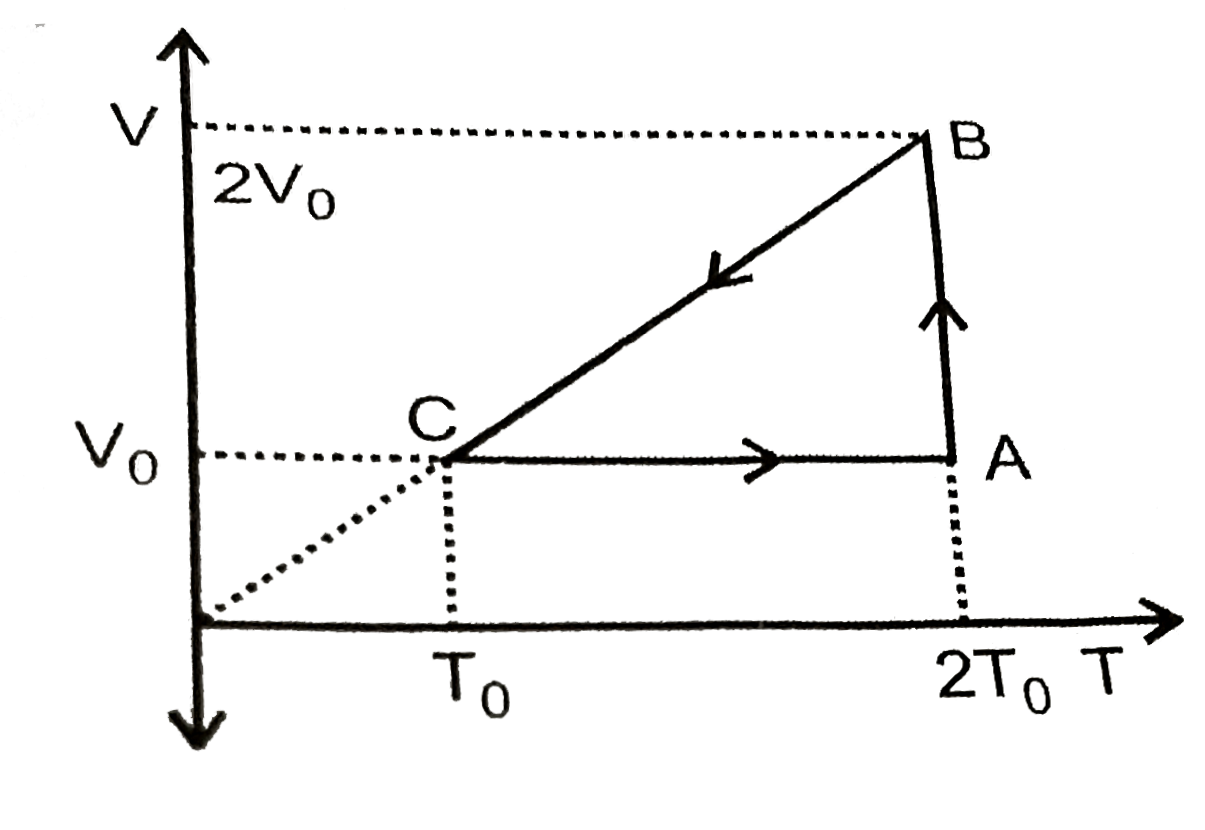
The correct Answer is:A

|

Answer

Step by step video, text & image solution for The efficiency of an ideal gas with adiabatic exponent 'gamma' for the shown cyclic process would be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Adiabatic exponent of a gas is equal to
A $C_{P} \times C_{V}$
B $\frac{C_{P}}{C_{V}}$
C $C_{P} - C_{V}$
D $C_{P} + C_{V}$
Question 2 - Select One
An ideal gas with adiabatic exponent ( $γ = 1.5$ ) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
AC=4R
BC=0
CC=2R
DC=R
Question 3 - Select One
An ideal gas with adiabatic exponent $γ$ undergoes a process in which internal energy depends on volume
as $U = a V^{α}$ then select the correct statement .
AChange in internal energy is $\frac{γ - 1}{α} Δ T$
BMolar heat capacity of process is $\frac{R}{1 - γ} + \frac{R}{α}$
CHeat exchange in the process is given by $Δ U [1 + \frac{1 - γ}{α}]$
DEquation of process is given is $P V^{x}$ =constant , where $x > 0 if α < 1$ .

DC PANDEY-SOLVD PAPERS 2017 NEET, AIIMS & JIPMER-Solved paper 2018(JIPMER)

Home
Ask Doubt
Profile