Two concentric spherical shells are as shown in figure. Match the following columns
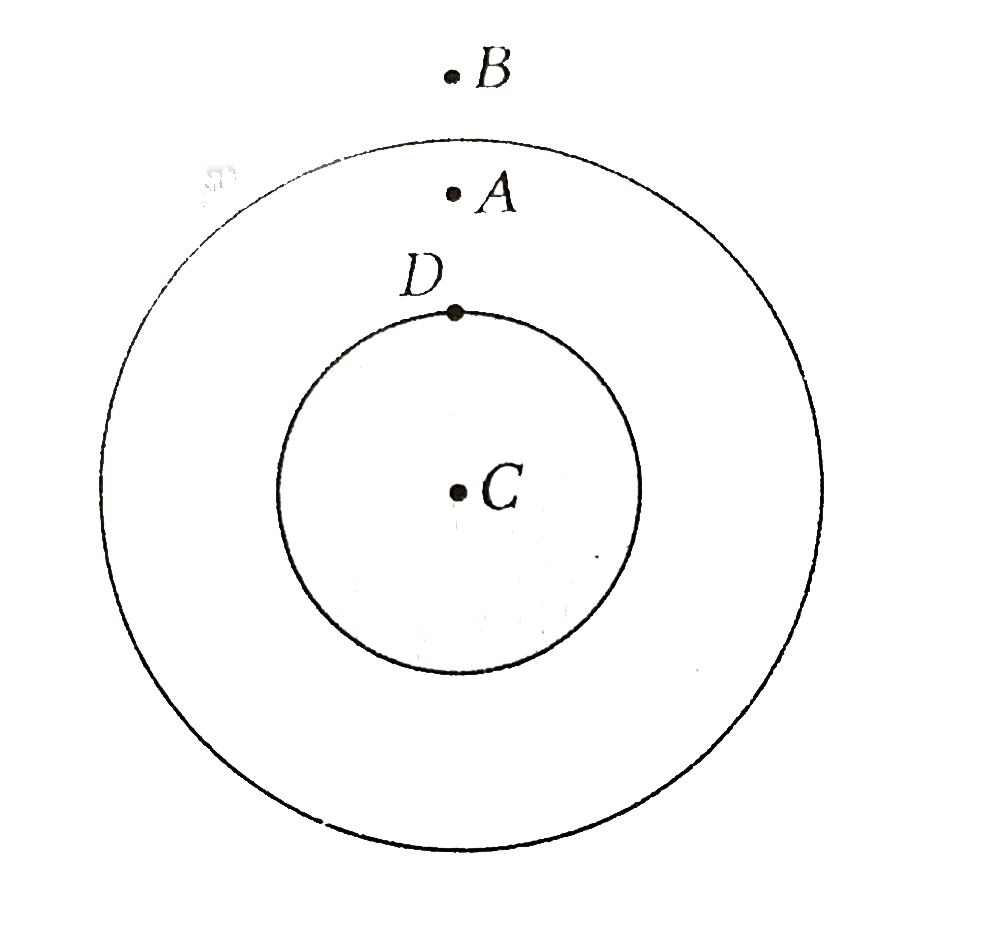
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)None
The correct Answer is:(A→q,B→t,C→r,D→s)
Inside a shell gravitational potential V=−GMR= constant
And gravitational field intensity E = 0
Outside the shell, V=−GMrandE=GMr2
As r increase, V=−GMrandE=GMr2
As r increase, V increase and E decreases
Therefore, potential at A. will be less than B. Gravitational field inside the shell will be zero. As one moves from C and D. the gravitational potential remains constant adn when one moves from D to A. gravitational field decreases.
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(A) Chapter Exercises
Explore 68 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
View SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four times
View Solution
Knowledge Check
Column IColumn II(A)Dimensional variable(p)π(B)Dimensionless variable(q)Force(C)Dimensional constant(r)Angle(D)Dimensionless constant(s)Gravitational constant
A-1B1/2C−1/2D1
Let V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
View SolutionMatch the following :
Column-1 Column-2(A)Electrostatic potential energy(P) Positive(B)Gravitational potential energy(Q) Negative(C)Elastic potential energy(R) Zero(D)Magnetic potential energy(S) Not defined
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionMatch the quantity of Column I with the quantity of Column II
Column IColumn II(A)Glycine(p)Has S-S linkage(B)Arginine(q)Optically active(C)Glutamic acid(r)Has pH less than 7(D)Cystine(s)Has pH greater 7
View SolutionOn the surface of earth acceleration due gravity is g and gravitational potential is V. Match of following columns
Column-IColumn-II(A)At height h=R, value of g(p)Decreases by a factor14(B)At depth h=R2,value of g(q)Decrease by a factor12(C)At height h=R,value of V(r)Increase by a factor118(D)At height h=R2,value of V(s)Increase by a factor 2(t)None
View SolutionMatch the following
Column-IColumn-II(A)Derived unit(p)Height(B)Fundamental unit(q)Thickness(C)Derived quantity(r)Area(D)Fundamental quantity(s)Newton(t)Kilogram
View SolutionMatch the following :
Column IColumn II(a)Penicillin(p)Bacteriostatic(b)Chloramphenicol(q)Antibiotic(c)Aspirin(r)Bacteriocidal(d)Ibuprofen(s)Analgesic(t)Antipyretic
View Solution