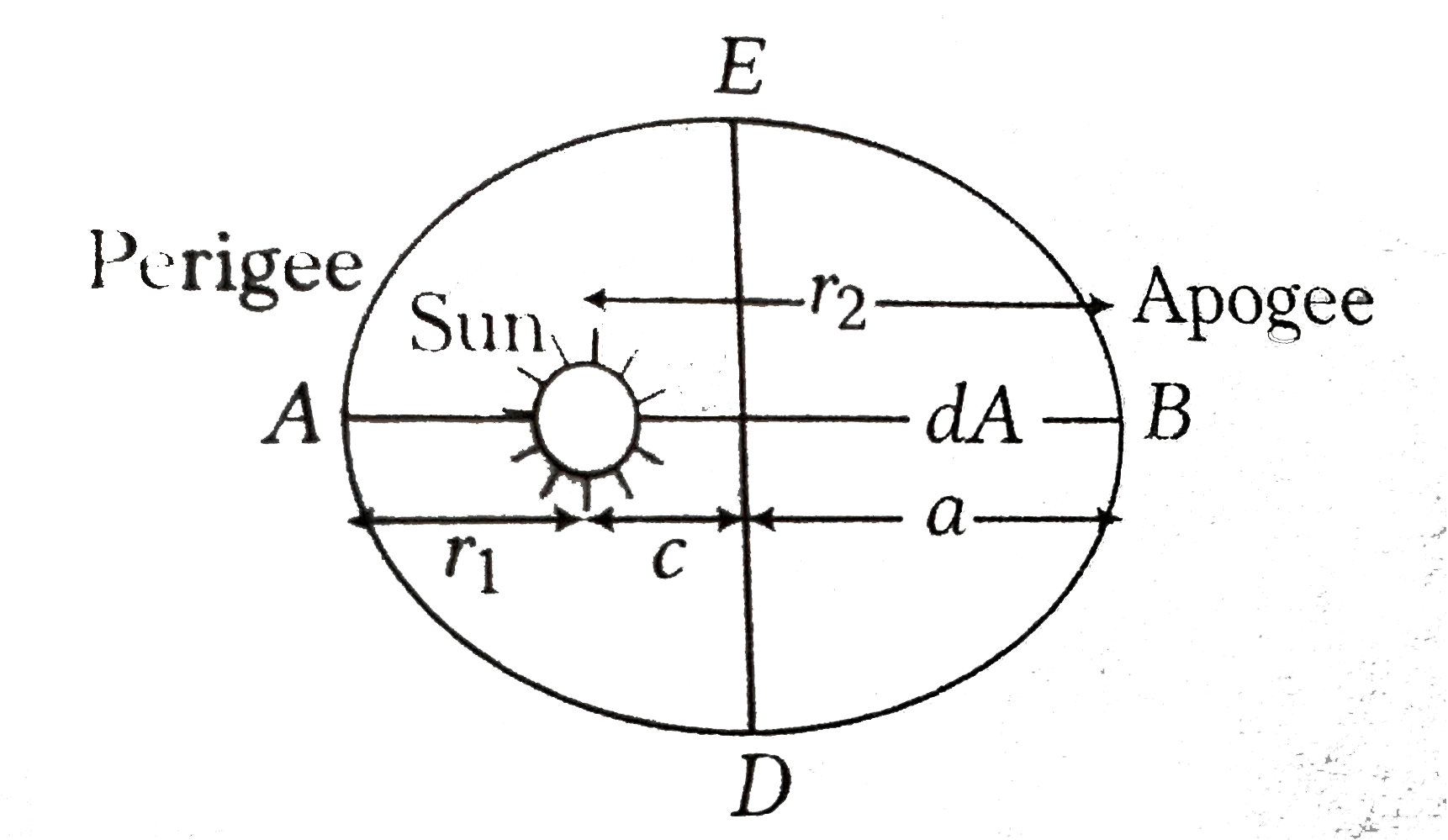
In elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
Column-IColumn-II(A)Speed of planet(p)Remains same(B)Distance of planet from centre of sun(q)Decreases(C)Potential energy(r)Increase(D)Angular momentum about centre of sun(s)Cannot say
The correct Answer is:(A→r,B→q,C→q,D→p)
In the figure given alongside, it can be seen that at perigee position, plant is nearest to the sun. So, in the elliptical moves, as the planet orbit from opogee position to perigee position, then speed of planet increases, distance of planet from cebtre of sun decreaes, potential energy decreases, Angular momentum about centre of sun remains the same
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
View SolutionMatch the following :
Column-1 Column-2(A)Electrostatic potential energy(P) Positive(B)Gravitational potential energy(Q) Negative(C)Elastic potential energy(R) Zero(D)Magnetic potential energy(S) Not defined
View Solution
Knowledge Check
Match the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2rA(A→s,B→r,C→p,D→q)B(A→c,B→s,C→p,D→q)C(A→s,B→r,C→q,D→p)D(A→q,B→r,C→p,D→s)
Match the following
Column-IColumn-II(A)Kepler's first law(p)T2∝r3(B)Kepler's second law(q)Areal velocity is constant(C)Kepler's third law(r)Orbit of planet is elliptical
View SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
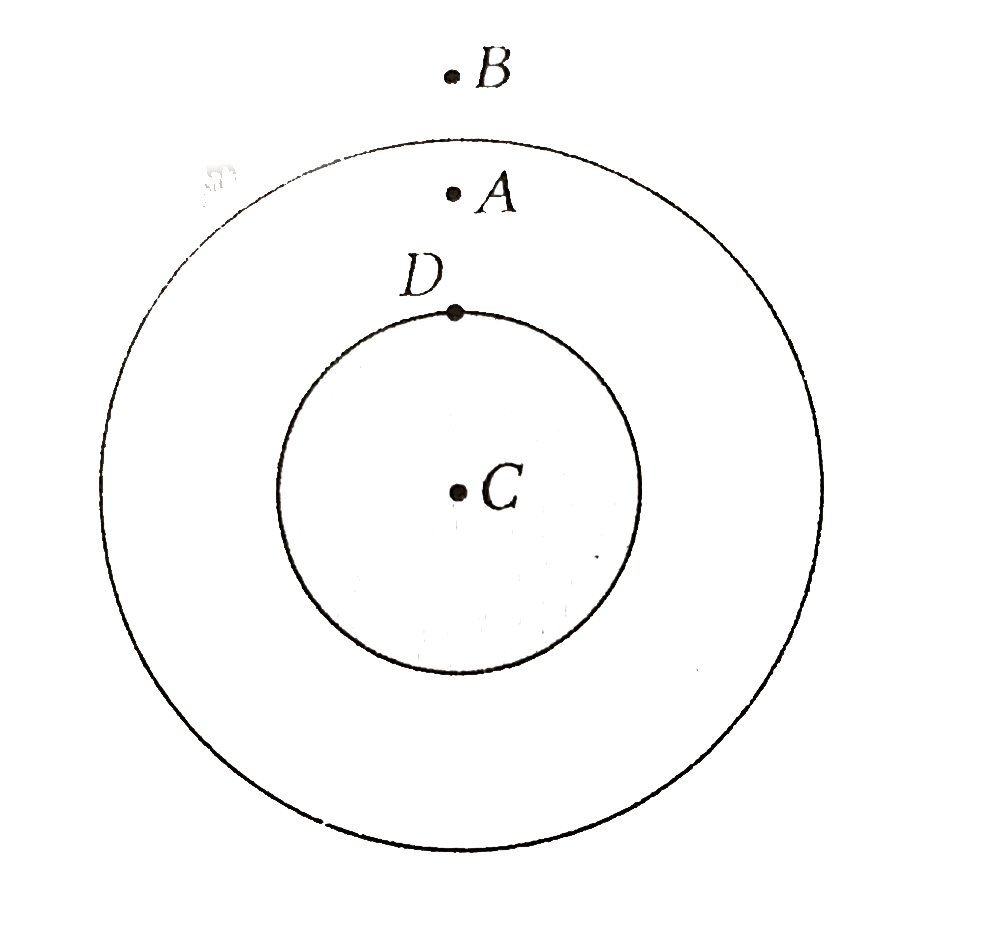
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)None
View SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four times
View SolutionMatch the following:
Column-IColumn-II(A)Water clock(p)Sand(b)Sun dial(q)flow of water(c)Hour glass(r)Shadow
View SolutionA planet moves in elliptical around sun, at one of focal points. Match the following, for different parameters related to the planet during the motion
Column IColumn II(A)Kinetic energy(p)Maximum at perigee(B)Gravitational potential energy(q)Minimum at perigee(C)Linear momentum(r)Maximum at apogee(D)Area swept per second radius(s)Minimum at apogee
View SolutionMatch the appropriate Column I with Column II.
Column IColumn II(A) Same dimension of mass(P) electric charge(B) Negative dimension of mass(Q) electric potential(C) Zero dimension of mass(R) electric capacity(D) Dimension of length is±D(S) energy density
View SolutionMatch the statements in Column I labeled as (a), (b), (c ), and (d) with those in Column II labeled as (p), (q), (r ), and (s). Any given statement in Column I can have correct matching with one or more statements in Column II.
An electron in hydrogen atom moves from n=1 to n=2.
Column IColumn II(a) Angular momentum(p) One-forth times(b) Kinetic energy(q) Two times(c) Potential energy(r) Four times(d) Mechanical energy(s) Half times
View Solution
