Calculate the index of refraction of a liquid from the following into glass:
(a) Reading for the bottom of an empty beaker: 11.324 cm
(b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm
(c) Reading for the upper level of the liquid in the beaker: 12.895cm
The correct Answer is:1.437
Step by step video, text & image solution for Calculate the index of refraction of a liquid from the following into glass: (a) Reading for the bottom of an empty beaker: 11.324 cm (b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm (c) Reading for the upper level of the liquid in the beaker: 12.895cm by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE F10videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE I12videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE A15videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - OPTICAL INSTRUMENTSEXERCISE - Problems for self practice35videos
OPTICAL INSTRUMENTS
- BOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE9videos
SOLIDS AND SEMICONDUCTOR DEVICES
Similar Questions
The apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionWhen half of the total volume of an empty beaker of mass 100 g is filled with water, its mass is found to be 500 g and when the remaining volume of the beaker is filled with a liquid, its mass is found to be 1 kg. Calculate the density of the liquid.
View Solution
Knowledge Check
- Question 1 - Select One
Calculate the index of refraction of a liquid from the following into glass:
(a) Reading for the bottom of an empty beaker: 11.324 cm
(b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm
(c) Reading for the upper level of the liquid in the beaker: 12.895cmA1.232B1.389C1.28D1.437 - Question 2 - Select One
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid?
 A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1
A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1 - Question 3 - Select One
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)
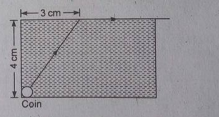
How fast is the light travelling in the liquid ?A1.8×108m/sB2.4×108m/sC3.0×108m/sD1.2×108m/s
While determining the refractive index of a liquid experimentally, the microscope was focussed at the bottom of a beaker, when its reading was 3.965 cm. on pouring liquid upto a height 2.537 cm inside the beaker, the reading of the refocussed microscope was 3.348 cm. Find the refractive index of the liquid.
View SolutionFind the apparent depth of an object O placed at the bottom of a beaker as shown in which two layers of transparent liquids are filled

[22.67 cm]View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light travelling in the liquid ?View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
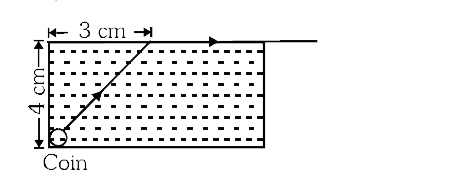
View Solution
A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be movedView Solution

